 |
MaGiX@LiX 2011 Abstracts |
 |
The FreeMABSys project and the Blad
librairies (Monday, 16h10–17h00). The FreeMabSys project aims at developing the FreeMabSys
library. This open source systems biology library evolves from the
Maple MabSys package. Models are implemented as
chemical reaction systems. They are analyzed by means of symbolic and
numeric methods. The FreeMabSys project is
supported by the ANR LEDA. In this talk, I will present our
motivations for the project and the functionalities of the open source
Blad libraries that are directly related to
FreeMabSys. These libraries are currently
incorporated to the Maple computer algebra software. I will try to
give some feedback about this experience and to highlight the good and
the not-so-good features of Blad.
Parallel programming with Sklml
(Thursday, 10h00–10h50). Writing parallel programs is
not easy, and debugging them is usually a nightmare. To cope with
these difficulties, the skeleton programming approach uses a
set of predefined patterns for parallel computations. The skeletons
are higher order functional templates that describe the program
underlying parallelism. Sklml is a new framework
for parallel programming that embeds an innovative compositional
skeleton algebra into the OCaml language. Thanks
to its skeleton algebra, Sklml provides two
evaluation regimes to programs: a regular sequential evaluation
(merely used for prototyping and debugging) and a parallel evaluation
obtained via a recompilation of the same source program in parallel
mode. Sklml was specifically designed to prove
that the sequential and parallel evaluation regimes coincide.
An OpenAxiom
Perspective on Pathways towards Dependable Computational
Mathematics (Thursday, 17h10–18h00). With
multicore processors becoming commodity, how can computational
mathematics spend Moore's dividend? I will present some perspectives
based on the development of the OpenAxiom
system. I will briefly discuss OpenAxiom's
architecture and challenges getting into the concurrency era. I will
present recent results and projects towards dependable computational
mathematics.
High Performance Implementation for Change of Ordering
of Zero-dimensional Gröbner Bases (Friday,
16h10–17h00). It is well-known that obtaining efficient
algorithms for change of ordering of Gröbner bases of 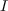 is crucial in polynomial system solving. This task is
classically tackled by linear algebra operations using the FGLM
algorithm. However, with recent progress on Gröbner bases
computations, this step turns out to be the bottleneck of the whole
solving process. Recently, Faugère and Mou proposed an
algorithm (Issac 2011) that takes advantage of
the sparsity structure of multiplication matrices appearing during the
change of ordering. This sparsity structure arises even when the input
polynomial system is dense. In practice, we obtain an implementation
which is able to manipulate 0
is crucial in polynomial system solving. This task is
classically tackled by linear algebra operations using the FGLM
algorithm. However, with recent progress on Gröbner bases
computations, this step turns out to be the bottleneck of the whole
solving process. Recently, Faugère and Mou proposed an
algorithm (Issac 2011) that takes advantage of
the sparsity structure of multiplication matrices appearing during the
change of ordering. This sparsity structure arises even when the input
polynomial system is dense. In practice, we obtain an implementation
which is able to manipulate 0 -dimensional
ideals over a prime field of degree greater than
-dimensional
ideals over a prime field of degree greater than 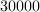 .
.
In this talk we report a high performance implementation of this
algorithm. Basic elementary steps were recoded to take advantage of
new features of recent Intel processors (SSE4 operations). Moreover,
the linear algebra library was upgraded to a multi-threaded
implementation. It out- performs by several order of magnitude the
Magma/Singular/FGb implementations of FGLM. For instance,
considering the problem of computing a Lex Gröbner basis from an
already computed DRL Gröbner basis of a system of 3 random
polynomials in 3 variables of degree 19 over 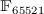 ,
it takes 1084.0 sec (resp. 8248.3 sec) with Magma (resp. Singular);
this time drops to 15.3 sec using the basic sequential C
implementation of the new algorithm. Finally, it takes only 0.71 sec
to achieve the same computation using a Bi QuadCore CPU with new
implementation.
,
it takes 1084.0 sec (resp. 8248.3 sec) with Magma (resp. Singular);
this time drops to 15.3 sec using the basic sequential C
implementation of the new algorithm. Finally, it takes only 0.71 sec
to achieve the same computation using a Bi QuadCore CPU with new
implementation.
Mickael Gastineau and Jacques Laskar
(IMCCE)
Trip (Monday,
14h50–15h40). Trip is a
computer algebra system that is devoted to perturbation series
computations, and specially adapted to celestial mechanics. Started in
1988 by J. Laskar, as an upgrade of
the special purpose Fortran routines elaborated
for the demonstration of the chaotic behavior of the Solar System,
Trip is now a mature tool for handling
multivariate generalized power series. Trip
contains also a numerical kernel and could be linked to other computer
algebra systems through the Scscp protocol.
Trip takes advantage of multiples cores
available on modern computers using the work-stealing techniques and
efficient memory management. We will present the design of Trip and the techniques used for the parallel
computations.
Scilab: What's new? (Tuesday,
16h10–17h00). Scilab is the free
numerical computation software for engineering and scientific
applications. Originally based on research at INRIA (the
French Research Institute for Computer Science and Automatic Control),
Scilab software has become the free reference in
numerical computation. Supported by a Consortium made of industrials
and academics and by a strong community of developers, Scilab
is used worldwide.
Scilab software is currently used in educational
and industrial environments around the world. There are more than
50,000 monthly remote loadings from the Web site of the Consortium.
About 80 countries download Scilab. Scilab includes hundreds of mathematical functions with
complete on-line help. It has an interpreter and a high level
programming language. Scilab language is made for easily performing
linear algebra and matrix computations. It allows making 2-D, 3-D
graphics, and animation. Scilab works under Windows XP/Vista/Seven,
GNU/Linux, and MacOSX. In the presentation we will first explain
briefly how we manage the process of free software development from
Research to business with the recent creation of
Scilab Enterprises Company. This process is completely based
upon the strategic orientation of the roadmap of Scilab,
mainly towards High Performance Computing and Embedded Systems. So we
will present what is new in Scilab today and
which are the future developments, stressing on future major
improvement: Scilab 6.
Macaulay2 (Thursday,
14h–14h50). I will discuss aspects of the design of the Macaulay2 user language that might be
useful in the Magix project and
assess their advantages and disadvantages based on the experience of
our users.
A TeXmacs tutorial (Wednesday,
11h10–12h00). TeXmacs is a free system for editing
technical documents available on Windows, MacOS-X and major Unix flavors.
It provides a structured view of the document and allow easy
management of various types of contents (text, graphics, mathematics,
interactive sessions, etc.) and easy customization via a macro system.
In this talk we will demonstrate the main features of this system, its
document format, its customization facilities and its interfacing
capabilities to external programs.
Fast Library for Number Theory: Flint (Tuesday, 9h30–10h20). Flint is a C library which offers fast
primitives for integer, polynomial and matrix arithmetic. We will
discuss some of the recent technological improvements in Flint and plans for the future. We will give an
overview of the various modules available in Flint
and discuss our approach to development, comparing the performance to
various other libraries.
Mathemagix Compiler (Thursday,
10h50–11h40). General purpose systems for computer algebra
such as Maple and Mathematica
incorporate a wide variety of algorithms in different areas and come
with simple interpreted languages for users who want to implement
their own algorithms. However, interpreted languages are insufficient
in order to achieve high performance, especially in the case of
numeric or symbolic-numeric algorithms. Also, the languages of the
Maple and Mathematics
systems are only weakly typed, which makes it difficult to implement
mathematically complex algorithms in a robust way.
Since one major objective of the Mathemagix
system is to implement reliable numeric algorithms, a high level
compiled language is a prerequisite. The design of the Mathemagix
compiler has been inspired by the high level programming style from
the Axiom and Aldor
systems, as well as the encapsulation of low level features by
languages such as C++. Moreover, the compiler
has been developed in such a way that it is easy to take advantage of
existing C++ template libraries. In our
presentation, we will give an overview of what has been implemented so
far and some of the future plans.
Semantic editing with GNU TeXmacs
(Friday, 10h50–11h40). Currently, there exists a big
gap between formal computer-understandable mathematics and informal
mathematics, as written by humans. When looking more closely, there
are two important subproblems: making documents written by humans at
least syntactically understandable for computers, and the formal
verification of the actual mathematics in the documents. In our talk,
we will focus on the first problem, by discussing some of the new
semantic editing features which have been integrated in the GNU
TeXmacs mathematical text editor.
To go short, the basic idea is that the user enters formulas in a
visually oriented (whence user friendly) manner. In the background, we
continuously run a packrat parser, which attempts to convert
(potentially incomplete) formulas into content markup. As long as all
formulas remain sufficiently correct, the editor can then both operate
on a visual or semantic level, independently of the low-level
representation being used. A related topic, which will also be
discussed, is the automatic correction of syntax errors in existing
mathematical documents. In particular, the syntax corrector that we
have implemented enables us to upgrade existing documents and test our
parsing grammar on various books and papers from different sources.
Mathemagix
libraries (Tuesday,
10h50–11h40). We will present the implementations of the
elementary operations with polynomials and matrices available in the
C++ libraries of Mathemagix. This
includes most of the classical methods for univariate polynomials and
series, but also very recent techniques with several variables.
Dedicated variants have been designed for numerical types. We will
illustrate some of the possibilities offered for certified numeric
computations with balls and intervals. Most of the algorithms can
benefit from parallelization and vectorization features now widely
spread in recent platforms.
This work is in collaboration with J. van der Hoeven.
The FreeMABSys project and the MabSys library
(Monday, 17h00–17h50). The FreeMABSys project aims at
developing the FreeMabSys library. This open
source systems biology library evolves from the Maple MabSys
package. Models are implemented as chemical reaction systems. They are
analyzed by means of symbolic and numeric methods. The FreeMabSys
project is supported by the ANR LEDA. In this talk, I will present the
MabSys package which is written in Maple. I will
show how the package can help modelling in Biology (and also for
studying dynamical systems with ODE) using approximate and exact
reductions. A software demo will be given.
Taylor models and their applications
(Monday, 14h00–14h50). The method of Taylor models
provides rigorous enclosures of functions over given domains, where
the bulk of the dependency is represented by a high order multivariate
Taylor polynomial, and the remaining error is enclosed by a remainder
bound. In this talk, we will discuss how to construct Taylor model
arithmetic on computers, which naturally includes integrations as a
part of arithmetic. Computations using Taylor models provide rigorous
results, and advantageous features of the method have shown to be able
to solve various practical problems that were unsolvable earlier. The
applications start from mere range bounding of functions, leading to
sophisticated rigorous global optimization, and especially the
fruitful is the use for rigorous solvers of differential equations.
Geometric computation behind Axel modeler
(Friday, 9h30–10h00). We discuss two specific
geometric algorithms in Axel
modeler, and their connection to Mathemagix.
First, a method for approximating planar semi-algebraic sets, notably
arrangements of curves. The method identifies connected components and
returns piece-wise linear approximations of them. Second, a framework
to compute generalized Voronoi diagrams, that is applicable to
diagrams where the distance from a site is a polynomial function
(Apollonius, anisotropic, power diagram etc). Computational needs
behind these methods are are mainly served by two Mathemagix packages: "realroot", for real solving, and
"shape",
for the geometric algorithms.
Optimizing computer algebra software for data locality
and parallelism (Tuesday, 14h00–14h50).
Parallel hardware architectures (multicores, graphics processing
units, etc.) and computer memory hierarchies (from processor registers
to hard disks via successive cache memories) impose an evolution of in
the design of scientific software. Algorithms for scientific
computation have often been designed with algebraic complexity as the
main complexity measure and with serial running time as the main
performance counter. On modern computers minimizing the number of
arithmetic operations is no longer the primary factor affecting
performance. Effective utilization of the underlying architecture
(reducing pipeline stalls, increasing the amount of instruction level
parallelism, better utilizing the memory hierarchy) can be much more
important.
This talk is an introduction to performance issues related to data
locality and parallelism for matrix and polynomial arithmetic
operations targeting multicore and GPU implementation. A first part
will be dedicated to data locality independently of parallelism thus
using serial algorithms and C programs as illustration. In a second
part analyzing and optimizing multithreaded programs on multicores
will be discussed. In the third part, we will switch to GPU specific
issues then compare the implementation techniques of both architecture
platforms.
Geometric Modeling and Computing with Axel (Wednesday, 10h00–10h50). Axel is an algebraic-geometric modeler
which allows to visualize and compute with different types of
tridimensional models of shapes. The main representations include
point sets, meshes, rational, bspline, algebraic and semi-algebraic
curves and surfaces. It is also a platform which integrates geometric
algorithms, through an open mechanisms of plugins. We will describe
its design, its extension mechanism, its main plugins, some of the
algorithms involved in the computation with semi-algebraic sets or
bsplines, and its connection with Mathemagix
Project.
Exact computations with an arithmetic known to be
approximate (Friday, 14h00–14h50).
Floating-point (FP) arithmetic was designed as a mere approximation to
real arithmetic. And yet, since the behaviour of each operation is
fully specified by the IEEE-754 standard for
floating-point arithmetic, FP arithmetic can also be viewed as a
mathematical structure on which it is possible to design algorithms
and proofs. We give some examples that show the interest of that point
of view.
Marc Pouzet (Univ. Pierre et Marie
Curie, ENS)
Some recent developments and extensions of Synchronous
Languages (Thursday, 12h00–12h50). Synchronous
languages were invented for programming embedded control software.
They have been used for the development of the most critical parts of
software in various domains, notably, avionics, power generation,
railways, circuits, etc.
The success of the original synchronous languages has spurred the
development of new languages, based on the same principles, that
increase modularity, expressiveness and that address new applications
like real-time video streaming, latency-insensitive designs, large
scale simulations, hybrid (continuous/discrete) systems.
Lucid Synchrone is one of these new
languages. It has served as a basis for experiment with several novel
extensions including, higher-order functions, type systems for the
clock calculus, hierarchical state machines with shared variables,
signals and new compilation methods. Many of these ideas have been
adopted in commercial tools, notably Scade 6.
New topics include techniques for allowing bounded desynchronisation
through buffers (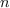 -synchrony) and extensions for
modeling continuous systems.
-synchrony) and extensions for
modeling continuous systems.
Exact computations and topology of plane curves
(Tuesday, 11h40–12h30). We will describe a new
algorithm for the computation of the topology of plane curves.
Such problems are usually solved by combining two kinds of algorithms:
those using exact computations (resultants, Sturm sequences, etc.) and
those using semi-numerical or numerical computations (approximations
of roots, refinements of +isolation boxes).
The global efficiency of the related solver is a balance between
symbolic computations (slow but giving a lot of certified
informations) and numerical computations (fast but eventually not
accurate or not certified) and is also a balance between the use of
asymptotically fast basic operations and more classical ones.
In this lecture, we will present a new global algorithm and fully
certified algorithm, including a new bivariate solver, and we will
explain our algorithmic choices (exact vs semi-numerical) as well as
some of our technical choices for the implementation (basic
algorithms, external libraries, multi-thread variants).
RAGlib: The Real Algebraic Geometry Library
(Tuesday 14h50–15h40). Most of algorithmic fundamental
questions in real algebraic geometry can be solved by the so-called
Cylindrical Algebraic Decomposition algorithm whose complexity is
doubly exponential in the number of variables. During the last 20
years, tremendeous efforts have led to algorithms based on the
so-called critical point method yielding much better complexity
results. RAGlib is an attempt to put into practice these more recent
techniques by implementing algorithms sharing some of the geometric
ideas who have led to theoretical complexity breakthroughs.
After a historical perspective, algorithms will be reviewed and some
applications that have been solved using RAGlib will be presented.
Efficiency questions will also be discussed and new functionalities
which will appear in the next release will be presented.
Anatomy of Singular
(Thursday, 14h50–15h40). I will present Singular and the parts it is composed of: memory
management, factorization, Groebner bases/algorithm of Mora,
interpreter, etc. The design decisions taken by the Singular group,
their problems and their advantages will be discussed.
We are just restructuring the code which converts these parts into
seperate libraries which may be used individually or together.
Although this is "work in progress" this set of libraries
may already be useful.
Accelerating lattice reduction with floating-point
arithmetic (Tuesday, 17h00–17h50). Computations
on Euclidean lattices arise in a broad range of fields of computer
science and mathematics. A very common task consists in transforming
an arbitrary basis of given lattice into a “nicer-looking”
one, made of somewhat orthogonal vectors. This reduction process,
whose most famous instance is LLL, heavily relies on Gram-Schmidt
Orthogonalisations. One can significantly accelerate lattice reduction
by replacing the rational arithmetic traditionally used for the
underlying GSO computations by approximate floating-point arithmetic.
In this talk, I will elaborate on this mixed numeric-algebraic
approach, which has been implemented in the fpLLL
library.
The cornerstone of lattice algorithmics is the famous LLL reduction
algorithm, which, despite being polynomial-time, remains somewhat
slow. It can be significantly speeded up by replacing the exact
rational arithmetic used for the underlying Gram-Schmidt computations,
by approximate floating-point arithmetic.
A natural means of speeding up an algorithm consists in working on an
approximation of the input with smaller bit-size and showing that the
work performed on the approximation is relevant for the actual exact
input. Unfortunately, a lattice basis that is close to an LLL-reduced
basis may not be itself LLL-reduced.
Cado-nfs: An
implementation of the Number Field Sieve (Friday,
17h00–17h50). The Number Field Sieve is the leading
algorithm for factoring large integers, and has been used over the
past 20 years to establish many records in this area. The latest of
these records is the factorization or rsa768 in 2010 by a joint effort
of several teams worldwide. We discuss in this talk several
algorithmic aspects of NFS, which are necessary features of a
state-of-the art implementation like Cado-nfs.
These different optimizations have all contributed greatly to the
success of the rsa768 factorization.
Éric Walter (Supelec, Univ.
Paris-Sud)
Interval Analysis for Guaranteed Set Estimation
(Monday, 11h40–12h30). Interval analysis (IA) makes it
possible to make proven statements about sets, based on approximate,
floating-point computations. It may thus be possible to prove that the
set of all solutions of a given problem is empty, or a singleton, or
to bracket it between computable inner and outer approximations. The
first part of this talk will present examples of problems in which one
is interested in sets rather than in point solutions. These examples
are taken from robotics, robust control and compartmental modeling
(widely used in biology). The basics of IA will be recalled in a
second part. Algorithms will be briefly presented that can be used to
find all solutions of sets of nonlinear equations or inequalities, or
all optimal estimates of unknown parameters of models based on
experimental data. These models may be defined by uncertain nonlinear
ordinary differential equations for which no closed form solution is
available. The third and last part of the talk will be a return on the
introductory examples, to see what can be achieved and what cannot,
what are the advantages and limitations of IA compared to alternative
technics and what are the challenges that IA must face to become part
of the standard engineering tools.
Stephen Watt (Univ. of Western
Ontario)
What Can We Learn from Aldor?
(Thursday, 16h20–17h10). It has now been two decades
since the work on Aldor began. From
its beginnings at IBM Research, through its further development by the
Numerical Algorithms Group and its use in research projects in Europe
and North America, Aldor has
explored the design space for programming languages in mathematical
computing. Many of the ideas seen in Aldor
have subsequently been adopted by more main-stream programming
languages, while others have not. In this talk we give a brief
overview of Aldor and what we see
as the most significant ideas it introduced. We go on to reflect on
what worked well, what didn't, and why.
The Mathematics of Mathematical Handwriting
Recognition (Friday, 11h00–11h40). Accurate
computer recognition of handwritten mathematics offers to provide a
natural interface for mathematical computing, document creation and
collaboration. Mathematical handwriting, however, provides a number of
challenges beyond what is required for the recognition of handwritten
natural languages. On one hand, it is usual to use symbols from a
range of different alphabets and there are many similar-looking
symbols. Mathematical notation is two-dimensional and size and
placement information is important. Additionally, there is no fixed
vocabulary of mathematical “words” that can be used to
disambiguate symbol sequences. On the other hand there are some
simplifications. For example, symbols do tend to be well-segmented.
With these characteristics, new methods of character recognition are
important for accurate handwritten mathematics input.
We present a geometric theory that we have found useful for
recognizing mathematical symbols. Characters are represented as
parametric curves approximated by certain truncated orthogonal series.
This maps symbols to a low-dimensional vector space of series
coefficients in which the Euclidean distance is closely related to the
variational integral between two curves. This can be used to find
similar symbols very efficiently. We describe some properties of
mathematical handwriting data sets when mapped into this space and
compare classification methods and their confidence measures. We also
show how, by choosing the functional basis appropriately, the series
coefficients can be computed in real-time, as the symbol is being
written and, by using integral invariant functions,
orientation-independent recognition is achieved. The beauty of this
theory is that a single, coherent view provides several related
geometric techniques that give a high recognition rate and that do not
rely on peculiarities of the symbol set.
A Foundation of Computable Analysis, the Representation
Approach (Monday, 10h50–11h40). Computable
Analysis studies all aspects of computability and complexity over
real-valued data. In 1955 A. Grzegorczyk and D. Lacombe proposed a
definition of computable real functions. Their idea became the basis
of the "representation approach" for computability in
Analysis, TTE (Type-2 Theory of Effectivity). TTE supplies a uniform
method for defining natural computability on a variety of spaces
considered in Analysis such as Euclidean space, spaces of continuous
real functions, open, closed or compact subsets of Euclidean space,
computable metric spaces, spaces of integrable functions, spaces of
probability measures, Sobolev spaces and spaces of distributions.
There are various other approaches for studying computability in
Analysis, but for this purpose, still TTE seems to be the most useful
one.
In TTE, computability of functions on the set of infinite sequences
over a finite alphabet is defined explicitly. Then infinite sequences
are used as “names” for “abstract” objects
such as real numbers, continuous real functions etc. A function on the
abstract objects is called computable, if it can be realized by a
computable function on names.
In the talk some basic concepts of TTE are presented and illustrated
by examples. Contents: Aims of computable analysis, The representation
approach (realization), Computable topological spaces, Representations
of subset spaces, Computable metric spaces, Computational complexity,
Final remarks.
Gnu Mpfr: back to the future
(Friday, 14h50–15h40). The first public version of Mpfr was released in February 2000.
Gnu Mpfr was developed after some long
discussions with specialists of floating-point arithmetic and
arbitrary precision, in particular Jean-Michel Muller and Joris van
der Hoeven. This talk will focus on the history of Mpfr and on the design decisions we took. We will
also detail some of the recent developments, and guess what Mpfr could be in 2022.
© 2011 Joris van der Hoeven
This webpage is part of the MaGiX
project. Verbatim copying and distribution of it is permitted
in any medium, provided this notice is preserved. For more
information or questions, please contact Joris van der
Hoeven.


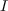 is crucial in polynomial system solving. This task is
classically tackled by linear algebra operations using the FGLM
algorithm. However, with recent progress on Gröbner bases
computations, this step turns out to be the bottleneck of the whole
solving process. Recently, Faugère and Mou proposed an
algorithm (
is crucial in polynomial system solving. This task is
classically tackled by linear algebra operations using the FGLM
algorithm. However, with recent progress on Gröbner bases
computations, this step turns out to be the bottleneck of the whole
solving process. Recently, Faugère and Mou proposed an
algorithm ( -dimensional
ideals over a prime field of degree greater than
-dimensional
ideals over a prime field of degree greater than 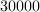 .
.
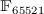 ,
it takes 1084.0 sec (resp. 8248.3 sec) with Magma (resp. Singular);
this time drops to 15.3 sec using the basic sequential C
implementation of the new algorithm. Finally, it takes only 0.71 sec
to achieve the same computation using a Bi QuadCore CPU with new
implementation.
,
it takes 1084.0 sec (resp. 8248.3 sec) with Magma (resp. Singular);
this time drops to 15.3 sec using the basic sequential C
implementation of the new algorithm. Finally, it takes only 0.71 sec
to achieve the same computation using a Bi QuadCore CPU with new
implementation.
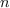 -synchrony) and extensions for
modeling continuous systems.
-synchrony) and extensions for
modeling continuous systems.