Title: Numerical approach of generalized
flatness
Keywords: symbolic-numeric computation, control theory,
modeling
Contacts
Address
1 rue Honoré d'Estienne d'Orves
91120 Palaiseau, France
Director of the laboratory: Mr Gilles Schaeffer <schaeffe@lix.polytechnique.fr>
Research team: MAX, Algebraic modeling and symbolic
computation
M2 students majoring in computer science or mathematics may apply.
Knowledge in at least one of the following topics is required: computer
algebra, differential algebra, control theory, numerical analysis. Basic
programming skills are also appreciated.
Applications should comprise a CV, a transcript of records, a letter of
motivation, and two recommendation letters. They should be sent to Joris van der Hoeven before April 21,
2025. Feel free to contact him for more information.
The MAX team is searching for PhD candidates on the themes of the ERC ODELIX project: solving differential equations fast,
precisely, and reliably. The present proposal concerns applications
of these themes to control theory.
Generic systems are not flat, but flatness is ubiquitous in engineering
[3]. This may require some simplifications of the model.
For examples, a classical aircraft model is flat if one neglects the
thrusts created by the actuators (ailerons, elevators, rudder) [4].
Flatness makes also easier to design a feed-back that can compensate
perturbations but also model errors [2].
In a recent paper, it has been proposed to improve the flat control of
an aircraft by using the values of the thrusts due to the actuators,
provided by the classical flat parametrization, to design a new more
accurate parametrization [5]. This process can be iterated
to produce a very precise motion planning for the aircraft model without
simplification.
The order of derivatives of the flat outputs required for such a
parametrization increases with the number of iterations, so that this
generalized flat parametrization depends potentially of an infinite
number of derivatives. One may conjecture that all systems would be flat
when allowing functions involving an infinite number of derivatives.
The goal is to investigate this notion of generalized flatness.
According to the taste and skills of candidates, this may be done in
many ways, focusing on computer experiments, or theoretical
investigations. Obviously some investment on computer simulations will
be required first to get an intuition relying on practical knowledge. On
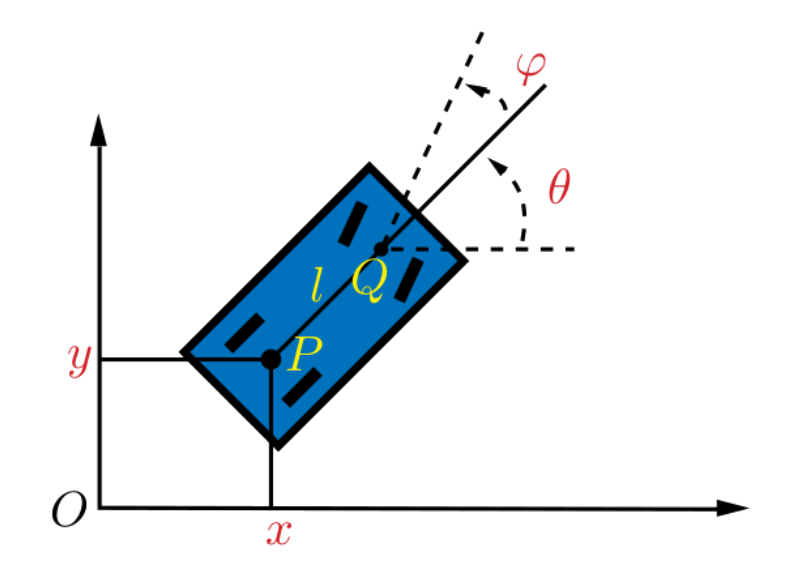
may consider for example a car with two trailers, that is flat if the
trailers are attached just above the rear axis, but not in the general
case [6]. A generalized flat parametrization may be
designed using iterations or homotopy methods, that is slowly moving the
points where trailers are attached.
One may also notice that generalized flatness allows to parametrize flat
systems, using a function that is not a genuine flat output. For
example, 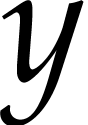 is a flat output for the system
is a flat output for the system 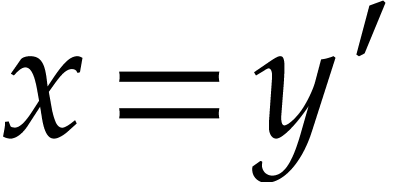 but not for the system
but not for the system 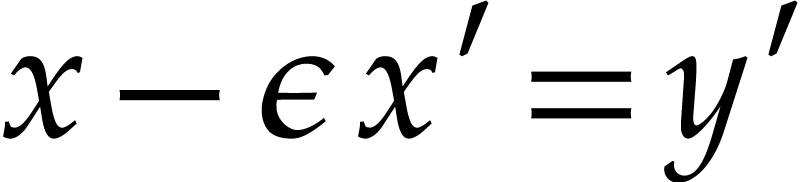 .
Anyway, one may use for small
.
Anyway, one may use for small 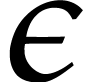 the
parametrization
the
parametrization  .
.
One may take advantage of existing implementations in Maple for the
aircraft and use the more efficient tools provided by Mathemagix. The
field of possible applications is large and include all non flat systems
and all flat ones for which one would like to use alternative sets of
functions that are not actual flat outputs.
The range of theoretical investigations is also very large, starting
with proofs of convergence. One may also consider the possible unicity
of this generalized flat parametrization.
Firstly, it will be necessary to deal with classical examples, such as
cars with trailers, through the creation of dedicated implementations.
This work should result in one or more publications.
Work more oriented towards computer science should include the creation
of efficient generic code, covering a large class of examples,
accompanied by a complexity analysis, benchmarks, and a study of the
precision of the results obtained. This will also give rise to one or
more publications.
We expect a minimal contribution to the theoretical setting, at least in
the linear case. Work more oriented towards the mathematical aspects of
control should focus on providing precise definitions and reporting
experimental behavior through proven statements, related to the
convergence of calculations and their precision.
Of course, the above list is purely indicative and may be adapted as a
function of the profile of the candidate. The software will be
distributed under a free software license and publications will take
place in prominent journals or conference proceedings of the area, such
as JSC, AAECC, ISSAC, etc.
-
[1]
-
Fliess, M., Lévine,
J., Martin, P., and Rouchon,
P. Flatness and defect of non-linear systems: introduction
theory and examples. Int. Journal of Control 61, 6 (1995),
1327–1361.
-
[2]
-
Kaminski, Y. and Ollivier,
F. Flat singularities of chained systems, illustrated with
an aircraft model. Computational and Applied Mathematics
43, 135 (2024).
-
[3]
-
Lévine, J. Analysis and
Control of Nonlinear Systems: A Flatness-based Approach.
Mathematical Engineering. Springer, 2009.
-
[4]
-
Martin, P. Aircraft control using
flatness. In CESA'96 – Symposium on Control, Optimization
and Supervision (Lille, France, 1996), IMACS/IEEE-SMC
Multiconference, 194–199.
-
[5]
-
Ollivier, F. Extending flat
motion planning to non-flat systems. experiments on aircraft
models using maple. In ISSAC '22: International Symposium on
Symbolic and Algebraic Computation, Villeneuve-d'Ascq, France,
July 4 - 7, 2022 (2022), Maza, M. M. and
Zhi, L., Eds., ACM, 499–507.
-
[6]
-
Rouchon, P., Fliess,
M., Lévine, J., and Martin, P. Flatness and motion planning: the car
with n trailers. In Proc. European Control Conference
(1993), 1518–1522.
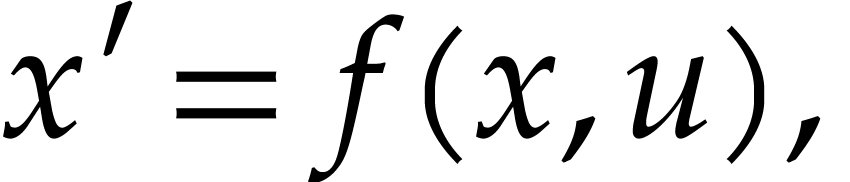
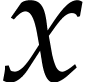 is a vector of state functions and
is a vector of state functions and
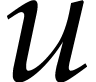 is a vector of control functions. This
system is said to be flat [1] if there exists
a local parametrization
is a vector of control functions. This
system is said to be flat [1] if there exists
a local parametrization 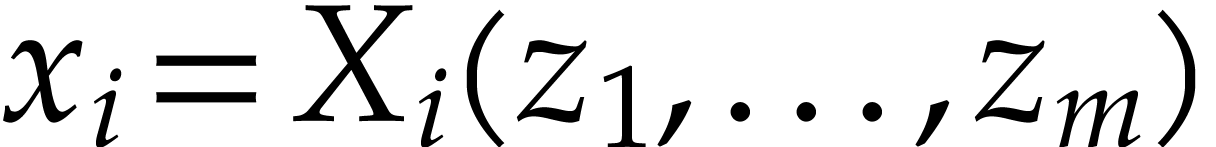 ,
where
,
where 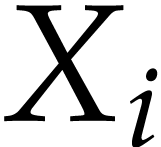 is a function of the functions
is a function of the functions 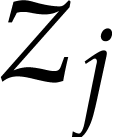 and of a finite number of their derivatives, and
the
and of a finite number of their derivatives, and
the 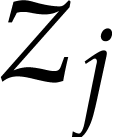 are functions of the time that may be
chosen arbitrarily. Furthermore, the
are functions of the time that may be
chosen arbitrarily. Furthermore, the 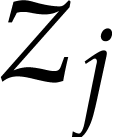 must be
expressed as differential functions of the state and the control:
must be
expressed as differential functions of the state and the control:
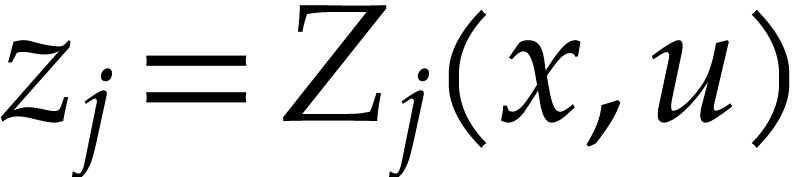 . These functions
. These functions 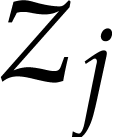 are called flat outputs.
are called flat outputs.
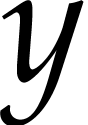 is a flat output for the system
is a flat output for the system 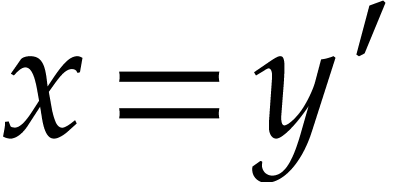 but not for the system
but not for the system 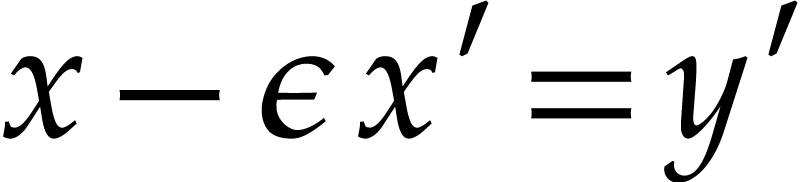 .
.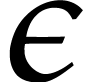 the
parametrization
the
parametrization  .
.