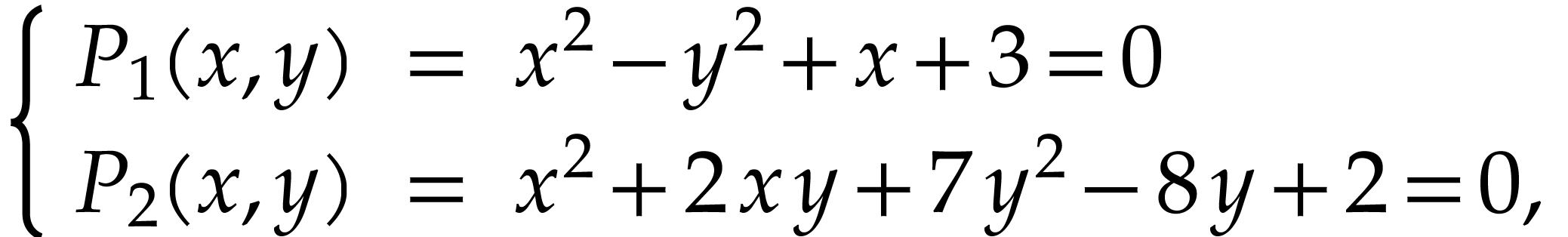
ODELIX — PhD proposal |
| WelcomeTeamPublicationsSoftwareEventsJobsInternships |
Title: Polynomial system solving using reliable numerical homotopy continuation
Keywords: symbolic and numeric algorithms; reliable computing; polynomial systems.
Contacts
Address
Director of the laboratory: Mr Gilles Schaeffer <schaeffe@lix.polytechnique.fr>
Research team: MAX, Algebraic modeling and symbolic computation
Applying |
M2 students majoring in computer science or mathematics may apply. Knowledge in at least one of the following topics is required: fast elementary algorithms, high performance computing, basic algebraic geometry.
Applications should comprise a CV, a transcript of records, a letter of
motivation, and two recommendation letters. They should be sent to Joris
Description |
Both in computer algebra and in numerical analysis, the resolution of systems of polynomial equations is a central problem. In computer algebra, this problem is often tackled using rewriting techniques, such as the computation of Gröbner bases or regular chains. In numerical analysis, one of the most successful methods is based on numerical homotopies. The idea is quite simple and goes as follows.
Starting with an input system, one first constructs a “simpler” system with the “same characteristics”. For instance, given the system
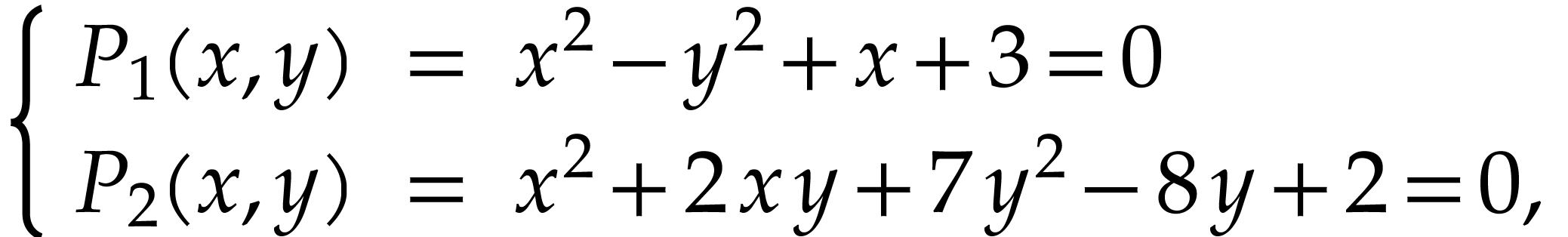 |
(1) |
we may for instance take
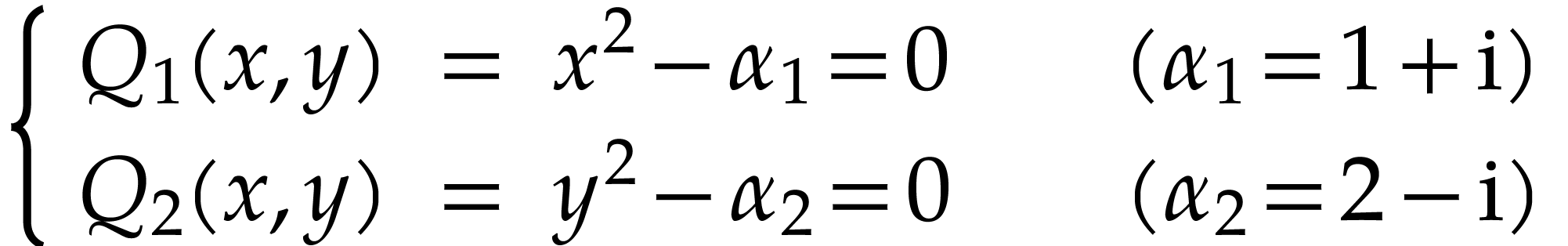 |
(2) |
for our simpler system. Both systems indeed have the “same
characteristics” in the sense that  and
and
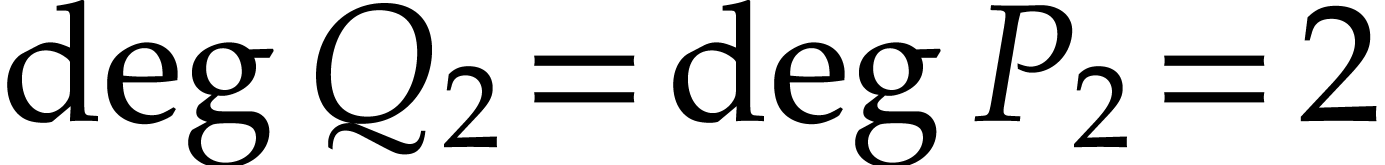 . In particular, we expect
both systems to admit the same number of solutions. By construction, the
solutions
. In particular, we expect
both systems to admit the same number of solutions. By construction, the
solutions 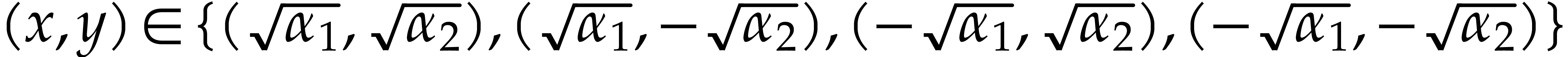 of (2) are easy to
compute. Now the main idea is to continuously deform the second system
into the first system using a homotopy continuation:
of (2) are easy to
compute. Now the main idea is to continuously deform the second system
into the first system using a homotopy continuation:
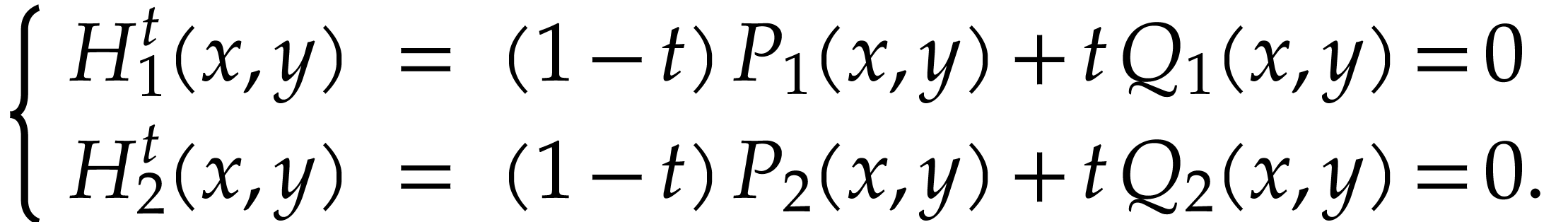 |
(3) |
Indeed, at 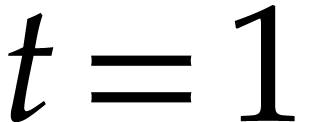 and
and 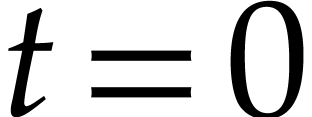 ,
the homotopy system (3) reduces to (2) and (1), respectively. In order to obtain the solutions of (1), it thus suffices to follow the solutions of (3)
from
,
the homotopy system (3) reduces to (2) and (1), respectively. In order to obtain the solutions of (1), it thus suffices to follow the solutions of (3)
from 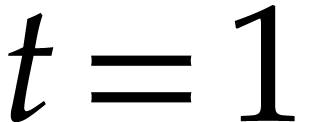 until
until 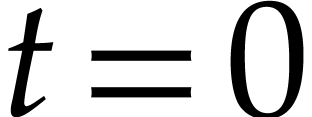 ,
using standard numerical algorithms. For instance, knowing the
approximate solutions of (1) at a given time
,
using standard numerical algorithms. For instance, knowing the
approximate solutions of (1) at a given time 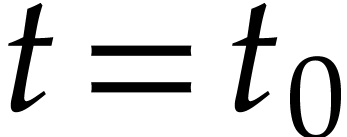 , we may find approximate solutions at
, we may find approximate solutions at 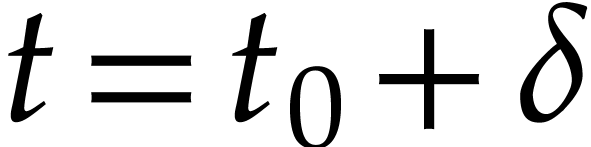 using Newton's method, starting with the
approximations at
using Newton's method, starting with the
approximations at 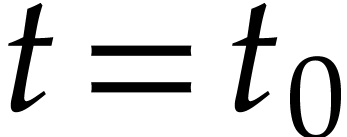 as our ansatz. It is
also possible to design higher order (e.g. Euler-type)
methods, which allow us to take larger steps
as our ansatz. It is
also possible to design higher order (e.g. Euler-type)
methods, which allow us to take larger steps 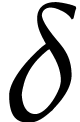 .
.
Context
There is an extensive literature on numeric homotopies [1,
3, 4, 20, 22].
Practical problems are usually not generic, which means that there may
be multiple solutions or solution paths 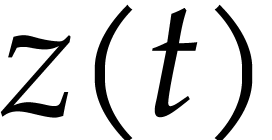 that go
to infinity (i.e. there are less isolated solutions than
predicted by the Bézout bound). Special strategies, called
end-games, need to be used near
that go
to infinity (i.e. there are less isolated solutions than
predicted by the Bézout bound). Special strategies, called
end-games, need to be used near 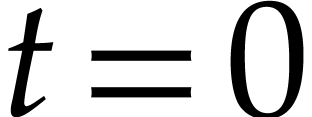 to cope
with multiple solutions. Solution paths that go to infinity typically
occur for sparse systems, when the supports of the polynomial
to cope
with multiple solutions. Solution paths that go to infinity typically
occur for sparse systems, when the supports of the polynomial 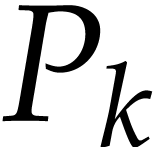 are special. Refinements of the Bézout bound exist
for this situation and special homotopies can be constructed that
preserve the support properties and the predicted number of solutions by
this refined bound. Finally, there exist several techniques to certify
the numeric solutions at
are special. Refinements of the Bézout bound exist
for this situation and special homotopies can be constructed that
preserve the support properties and the predicted number of solutions by
this refined bound. Finally, there exist several techniques to certify
the numeric solutions at 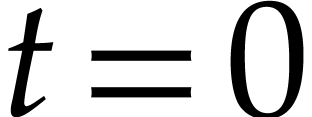 [7, 9, 14, 19] or all along the path [2, 6, 9, 23].
[7, 9, 14, 19] or all along the path [2, 6, 9, 23].
In favorable cases, existing software for numeric homotopies [1, 5, 16, 17, 21] is many times faster than symbolic software for the computation of Gröbner bases. However, many things can go wrong during numeric path tracking: there might be singularities on or near the paths, end-games for high multiplicities may incur a large performance penalty, the working precision might be insufficient, the numeric conditioning might be bad, etc. Existing software packages typically require manual fine-tuning of internal parameters in order to treat the most interesting examples.
In the context of the ERC ODELIX project (of which this proposal is a part), we are interested in polynomial systems that are verified by the coefficients of truncated power series solutions of differential equations. Such systems come with a special structure that we wish to understand better and then exploit.
Methodology |
The thesis will begin by gathering state of the art literature on numerical polynomial system solving, along with software implementation. We will focus on the case of square homogeneous systems with regular solutions. More specifically, building on [9], the following theoretical question will be addressed: How to perform reliable homotopy continuations in the most efficient way?
The second part of the thesis will be devoted to non-regular solutions (what are the most efficient methods to numerically compute multiple zeros and certify them?) and systems that arise from differential equations (how to exploit this special structure and what is the complexity of homotopy continuation for this application?).
The practical component of the thesis concerns the software
implementation of reliable homotopy methods. We intend to distribute the
implementation inside a dedicated library as free software under the GNU
General Public License. Several tools for reliable arithmetic are
already available in
More specifically, we plan to work on the following implementation issues:
Development of algorithms for the efficient evaluation of the input polynomials for various numerical and reliable data types, possibly using automatic code generation and just-in-time compilation.
Implementation of additional reliable data types for the efficient certification of numeric homotopy steps, such as special kinds of Taylor models [18] and ball arithmetic [11].
Development of multi-threaded homotopy solvers.
Make the homotopy solvers benefit from hardware SIMD (Single
Instruction Multiple Data) vector instructions, potentially based on
tools available in the
Expected results |
Concerning the theoretical part, a first article will be devoted to a new algorithm for the reliable solving of square homogeneous systems with regular solutions, along with a prototype software implementation: the complexity will be parametrized by condition numbers and should not exceed the worst case bounds proved by Shub and Smale.
Subsequent theoretical papers will concern multiple and clustered solutions and/or applications to differential equations. The theoretical papers will be submitted to journals or conferences in computer algebra or reliable computing.
The practical counterpart will be a high-level solver that automatically selects the most efficient low-level method(s) for solving the specific input problem. In particular, it should not require any manual fine-tuning of parameters or verifications that we are indeed in a zone where numerical correctness is guaranteed. In addition it should compete with the best purely numerical implementations. The final software library is expected to be presented in a wide audience journal such as ACM Transactions on Mathematical Software.
Bibliography |
D. J. Bates, J. D. Hauenstein, A. J. Sommese, and C. W. Wampler. Numerically Solving Polynomial Systems with Bertini. SIAM, 2013.
C. Beltrán and A. Leykin. Robust certified numerical homotopy tracking. Found. Comput. Math., 13(2):253–295, 2013.
C. Beltrán and L. M. Pardo. Fast linear homotopy to find approximate zeros of polynomial systems. Found. Comput. Math., 11:95–129, 2011.
L. Blum, F. Cucker, M. Shub, and S. Smale. Complexity and real computation. Springer-Verlag, 1998.
P. Breiding and S. Timme. Homotopycontinuation.jl: a package for homotopy continuation in Julia. In International Congress on Mathematical Software, pages 458–465. Springer, 2018.
J. D. Hauenstein, I. Haywood, and A. C. Liddell. An a posteriori certification algorithm for Newton homotopies. In Proc. ISSAC '14, ISSAC '14, pages 248–255. New York, NY, USA, jul 2014. ACM.
J. D. Hauenstein and F. Sottile. Algorithm 921: AlphaCertified: certifying solutions to polynomial systems. ACM Trans. Math. Softw., 38(4):28–1, 2012.
J. van der Hoeven. Journées Nationales de Calcul Formel (2011), volume 2 of Les cours du CIRM, chapter Calcul analytique. CEDRAM, 2011. Exp. No. 4, 85 pages, http://ccirm.cedram.org/ccirm-bin/fitem?id=CCIRM_2011__2_1_A4_0.
J. van der Hoeven. Reliable homotopy continuation. Technical Report, HAL, 2011. https://hal.archives-ouvertes.fr/hal-00589948.
J. van der Hoeven and G. Lecerf. Faster FFTs in medium precision. In 22nd IEEE Symposium on Computer Arithmetic (ARITH), pages 75–82. June 2015.
J. van der Hoeven and G. Lecerf. Evaluating straight-line programs over balls. In 23nd IEEE Symposium on Computer Arithmetic (ARITH), pages 142–149. 2016.
J. van der Hoeven, G. Lecerf, B. Mourain, Ph. Trébuchet, J. Berthomieu, D. Diatta, and A. Mantzaflaris. Mathemagix, the quest of modularity and efficiency for symbolic and certified numeric computation. ACM SIGSAM Communications in Computer Algebra, 177(3), 2011. In Section "ISSAC 2011 Software Demonstrations", edited by M. Stillman, p. 166–188.
J. van der Hoeven, G. Lecerf, and G. Quintin. Modular SIMD arithmetic in Mathemagix. ACM Trans. Math. Softw., 43(1):5–1, 2016.
R. Krawczyk. Newton-algorithmen zur Bestimmung von Nullstellen mit Fehler-schranken. Computing, 4:187–201, 1969.
G. Lecerf. New recombination algorithms for bivariate polynomial factorization based on Hensel lifting. AAECC, 21(2):151–176, 2010.
T.-L. Lee, T.-Y. Li, and C.-H. Tsai. Hom4ps-2.0: a software package for solving polynomial systems by the polyhedral homotopy continuation method. Computing, 83(2):109–133, 2008.
A. Leykin. Polynomial homotopy continuation in Macaulay2. ACM Communications in Computer Algebra, 50(3):113–116, 2016.
K. Makino and M. Berz. Remainder differential algebras and their applications. In Computational differentiation: techniques, applications and tools, pages 63–74. SIAM, Philadelphia, 1996.
S. M. Rump. Kleine Fehlerschranken bei Matrixproblemen. PhD thesis, Universität Karlsruhe, 1980.
A. J. Sommese and C. W. Wampler. The Numerical Solution of Systems of Polynomials Arising in Engineering and Science. World Scientific, 2005.
J. Verschelde. Algorithm 795: PHCPACK: A general-purpose solver for polynomial systems by homotopy continuation. ACM Transactions on Mathematical Software, 25(2):251–276, 1999.
J. Verschelde. PHCpack: a general-purpose solver for polynomial systems by homotopy continuation. ACM Transactions on Mathematical Software, 25(2):251–276, 1999. Algorithm 795.
J. Xu, M. Burr, and C. Yap. An approach for certifying homotopy continuation paths: univariate case. In Proc. ISSAC '18, ISSAC '18, pages 399–406. New York, NY, USA, jul 2018. ACM.