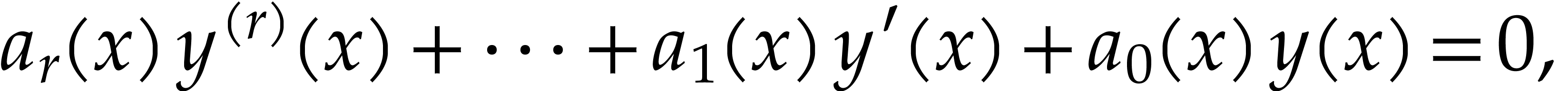
ODELIX — PhD proposal |
| WelcomeTeamPublicationsSoftwareEventsJobsInternships |
Title: Complexity of solving linear differential equations
Keywords : computer algebra, symbolic-numerical algorithms, reliable computing, ordinary differential equations, high performance computing.
Contacts
Address
Director of the laboratory: Mr Gilles Schaeffer <schaeffe@lix.polytechnique.fr>
Research team: MAX, Algebraic modeling and symbolic computation
Applying |
M2 students majoring in computer science or mathematics may apply. Candidates must be familiar with computer algebra and complex analysis. Knowledge of high performance computing or differential Galois theory is an optional advantage.
Applications should comprise a CV, a transcript of records, a letter of
motivation, and two recommendation letters. They should be sent to Joris
Context |
In the area of computer algebra, one is interested in exact algorithms for the manipulation of mathematical objects such as polynomials, matrices or algebraic numbers. The expression “exact manipulation” covers roughly the calculations that a mathematician could make with a paper and pencil, and is opposed to approaches based on discretization and of central numerical approximations in scientific computing.
However, formal and numerical calculation are not exclusive. The approximation of numbers with arbitrary precision is an essential functionality of computer algebra software, and, increasingly, these offer tools for rigorous numerical calculation, that is to say where the results are accompanied by error bounds. The techniques involved in rigorous and arbitrary precision computations approach those of symbolic calculation. More broadly, the so-called symbolic-numerical algorithms exploit the complementarity between exact methods (more easily rigorous, better able to deal with singular or poorly conditioned problems) and numerical (often more efficient and more widely applicable). It is this type of mixed approach that this thesis project aims to explore.
The central question of this proposal concerns the efficient numerical resolution of linear differential equations
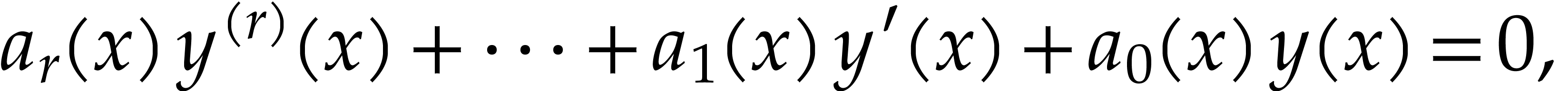 |
(1) |
where the functions 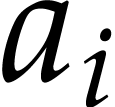 are typically polynomials
with rational coefficients. Equations of this type are omnipresent in
the theory of special functions, and appear naturally in physics, but
also for example in combinatorics (finite differential generating
series) or in algebraic geometry (Picard-Fuchs equations).
are typically polynomials
with rational coefficients. Equations of this type are omnipresent in
the theory of special functions, and appear naturally in physics, but
also for example in combinatorics (finite differential generating
series) or in algebraic geometry (Picard-Fuchs equations).
For these equations, numerical resolution algorithms are available that
go beyond the generic methods of numerical analysis. For example, it is
now well known that when equation (1) and the point where
we want to evaluate its solution are fixed, we can approximate the
corresponding value with an absolute error of at most 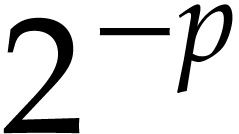 in only
in only 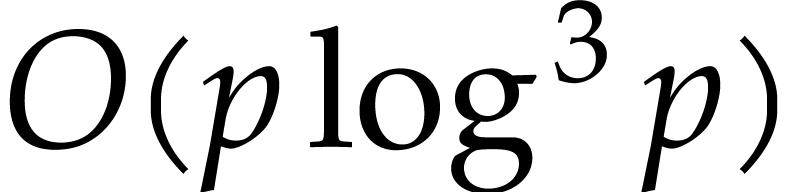 operations when
operations when 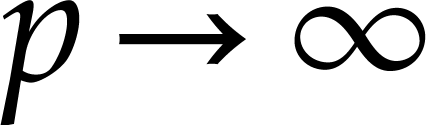 . On the other hand, the dependence of this cost on
the size of the equation has not been completely analyzed. The same goes
for the dependence on the evaluation point, which involves subtle
analytical phenomena when it approaches a point where the equation is
singular.
. On the other hand, the dependence of this cost on
the size of the equation has not been completely analyzed. The same goes
for the dependence on the evaluation point, which involves subtle
analytical phenomena when it approaches a point where the equation is
singular.
One of the motivations for analyzing in detail the cost of solving linear differential equations is that it constitutes a step for other algorithms, including algorithms whose input and output are purely algebraic. In particular, solving an equation numerically can be used to solve it exactly! Several works in recent years have focused, for example, on factoring linear differential operators — a step in the search for exact solutions — from the data of the monodromy matrices and the Stokes matrices of the corresponding equation, two families of matrices that are expressed in terms of solution values. The lack of control over the cost of the numerical step is one of the things that blocks the complexity analysis of these algorithms.
Subject of the PhD |
The main aim of this thesis is to better understand the complexity, i.e. the cost in computation time, of the numerical resolution of equations of the form (1). One may both intend to refine the analysis of existing algorithms and to develop algorithms with a better complexity whenever possible. Some particularly interesting questions are the following:
Bound the cost to compute monodromy matrices or Stokes matrices of a linear differential equation as a function of its size (order, degree, coefficient size) and the required precision.
Understand how to refine these bounds in the presence of information on the analytical behavior of the solutions.
Make complexity analyses reflect the practical behavior of the implementations. Exploit progress in our theoretical understanding in order to develop more efficient practical solvers, possibly integrating new algorithms.
A second goal concerns the study of the complexity of “exact resolution” algorithms based on the numerical computation of solutions. For each problem, such as the factorization of operators, the following questions arise:
What is the numerical precision required to guarantee that the desired result has been obtained?
Based on this precision and given the results on the numerical resolution part, what is the total cost of the algorithm? How does this cost compare to that of purely algebraic algorithms for the same task?
Finally, depending on the interests of the PhD student and the initial results obtained, the research may move in other directions related to the previous ones, such as the following:
Develop a new particular efficient solver for small and medium precisions, while exploiting the parallelism (SIMD and multicore) inside modern computers.
Better determine the scope of the symbolic-numerical approach when applied to exact resolution: when does this approach allow going beyond what is possible with known purely algebraic techniques? In which cases do finite precision numerical calculations give rise to complete algorithms, and in which cases must we rely on heuristic methods?
Expected results |
We consider the thesis a success if significant progress is made in one or more of the directions listed above and published in reference journals or conference proceedings in our field. New software that improves the practical efficiency of numerical integration of linear differential equations would be a highly appreciated bonus.
Bibliography |
A.
F.
D. V.
D. V.
J. 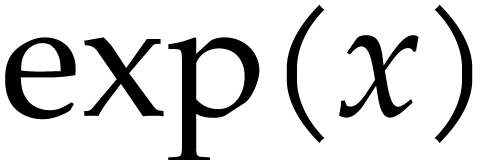 with
precomputations,” in 2024 IEEE 31st Symposium on Computer
Arithmetic (ARITH), Malaga, Spain: IEEE, Jun. 2024, pp. 80–87.
doi: 10.1109/ARITH61463.2024.00023.
with
precomputations,” in 2024 IEEE 31st Symposium on Computer
Arithmetic (ARITH), Malaga, Spain: IEEE, Jun. 2024, pp. 80–87.
doi: 10.1109/ARITH61463.2024.00023.
J.
J.
J.
J.
P.
A.
A.
M.