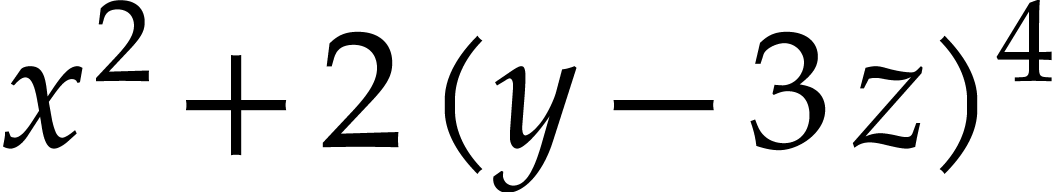Title: Straight-line programs, extreme performance, and applications

Keywords: high performance computing; symbolic computation; reliable computing; compilation; straight-line programs

Contacts

Address

Director of the laboratory: Mr Gilles Schaeffer <schaeffe@lix.polytechnique.fr>

Research team: MAX, Algebraic modeling and symbolic computation

M2 students majoring in computer science or mathematics may apply. Knowledge in most of the following topics is required: compilers, high performance computing, programming on GPUs, computer algebra and arithmetic, fast elementary algorithms, complexity theory, C++.

Applications should comprise a CV, a transcript of records, a letter of motivation, and optional recommendation letters. They should be sent to Joris van der Hoeven before October 1, 2024. Feel free to contact him for more information.

Consider the simplest kind of numerical problems that one can build on a CPU using a sequence of arithmetic operations on floating point numbers and without any non-trivial control structures. We call them straight-line programs or SLPs [2]. More generally, one may consider any finite set of “basic” operations (instead of the arithmetic operations) on a “basic” data type (instead of machine floating point numbers).

For instance, the following SLP can be used to compute the function :

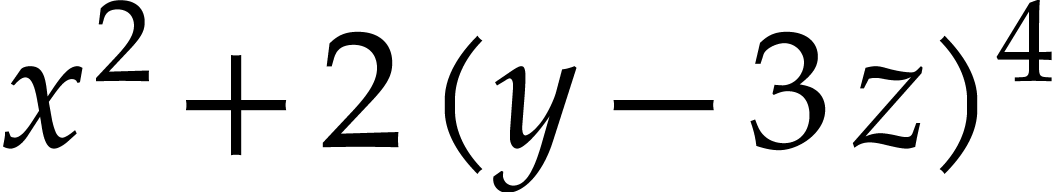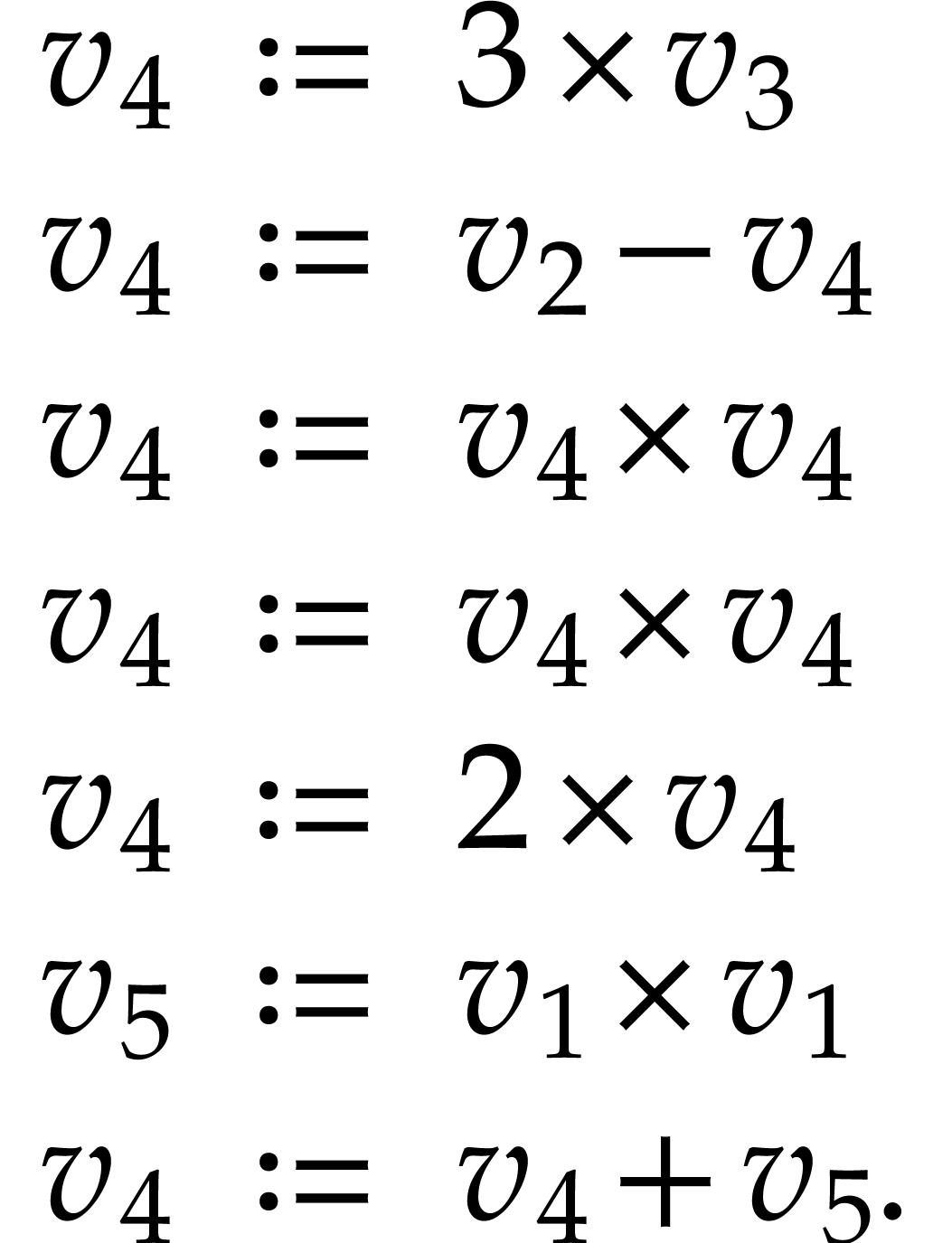
Here are a finite number of “registers” that we use to contain our data (floating point numbers). Some of these registers correspond to the input of our SLP (namely 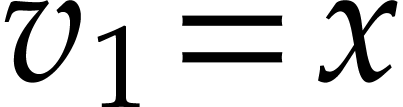, , 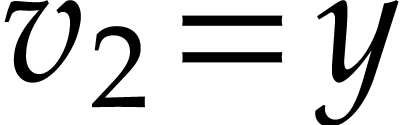and 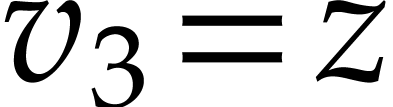) and some of them to the output (namely 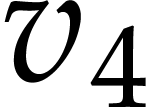). The arguments of the instructions are either registers or constants (such as and ).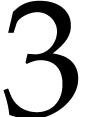

On the one hand, SLPs can naturally be considered as a data type. For instance, the above program is one possible representation of the polynomial 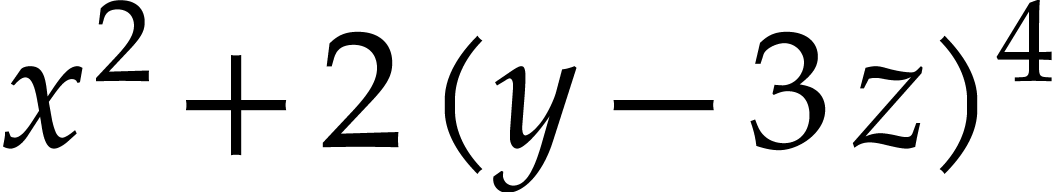and it is natural to support this representation in libraries dedicated to computations with multivariate polynomials. On the other hand, SLPs can be regarded as programs. Consequently, we may use techniques from compilers to perform basic tasks on SLPs, such as common subexpression elimination, register allocation, or the generation of bytecode that can directly be executed on the CPU.

The main aim of this thesis is to develop and implement extremely efficient algorithms for many computations with SLPs, by exploiting their specific advantages:

• Contrary to general purpose programs, SLPs can be represented in simple ways that are suitable for efficient manipulations.

• The absence of non-trivial control structures also makes it possible to specialize general purpose compilation techniques to obtain further efficiency gains.

• Although the formalism SLPs is limited and highly constrainted by design, it does allow for arbitrary sets of basic operations and arbitrary basic data types. For several basic types of interest, this makes it possible to develop specific mathematical optimizations that would be hard to achieve for general purpose programs [5].

• The simplicity of the formalism invites us to investigate and support more exotic types of hardware, such as GPUs, matrix coprocessors, or large networks.

• Despite their simplicity, SLPs admit many interesting applications. In particular, we will explore the integration of ordinary differential equations, homotopy continuation, and sparse interpolation. SLPs are also naturally encountered for general purpose applications whenever it is possible to unroll all loops and function calls.

Many applications that use SLPs provide ad hoc implementations of a few particularly useful functionalities. For instance, homotopy continuation software typically comes with some support for the computation of symbolic Jacobians and for the homogenization of multivariate polynomials. Such algorithms are typically pleasant to implement due to the simplicity of SLPs. In particular, there often exist linear or quasi-linear time algorithms that can be implemented without excessive efforts.

However, naive implementations may not exploit all advantages of this simplicity: they are typically written in a high level language and may not go as far as generating efficient machine code on the fly. When binary code is produced using a traditional C compiler, the compilation time is typically much higher than necessary. Optimizations for SLPs may also be limited to a few standard techniques, without exploiting the full potential of mathematical properties of particular data types. Finally, implementations are often limited to one particular type of hardware that the programmar is most familiar with.

The aim of this thesis is to design and implement a stand-alone C++ library for SLPs that is both extremely efficient and versatile. Wrappers for several languages will be provided such that implementations that require SLPs can easily rely on this library.

The thesis will start with a survey of existing techniques: traditional theory of compilers [1], complexity theory [2], computer algebra [3], familiarization with various types of hardware, etc. This will be done in parallel with a careful study of efficiency of various representations of SLPs through the implementation of basic known algorithms. One particular challenge is to reduce the time to perform basic transforms on SLPs to only a factor between 10 and 1000 times to execute the corresponding machine code. This will also be the occasion to carefully examine timings for different types of hardware.

Our second objective is the design and implementation of efficient algorithms for SLPs over specific data types like intervals and balls, multi-precision numbers (both integers, fixed point, and floating point numbers), modular numbers, truncated power series, matrices, etc. This includes a close examination of mathematical properties that can be exploited to design specific optimizations for these data types.

As the thesis goes on, we also hope to obtain a better understanding of the theoretical power of the computational model of SLPs. For instance, to which extent would it be a good idea to dynamically unroll general purpose algorithms from computer algebra as SLPs instead of relying on a traditional implementation? To what extent can SLPs be used a simplified model for parallel computations on GPUs and distributed hardware? How easily can good properties of the computational model of SLPs be extended to slightly more general models?

Throughout the thesis, a lot of attention will be paid to high quality implementations that demonstrate the theoretical claims and that will be distributed through a stand-alone and freely distributed C++ software library.

The theoretical part of the research should lead to a series of at least three papers (one every year) on more efficient algorithms for SLPs, along the lines sketched above. This work should be published in major journals of our area (like JSC, AAECC, Journal of Complexity, etc.) or in the proceedings of major conferences (like ISSAC, ARITH, etc.). We also expect one or more papers dedicated to applications such as multiple precision arithmetic, differential equations, homotopy continuation, or sparse interpolation.

The practical part of the PhD is expected to lead to a high performance C++ library for computations with SLPs. The library should be efficient both for internal computations on SLPs and for the execution of machine code that can be produced on the fly. The library should also be versatile both when it comes to the supported data types and the kinds of hardware on which the SLPs can be executed.

All software will be released under a free software license and wrappers will be written to use it from higher level languages such as Mathemagix [6] or Julia. Special support will also be include it in order to use in combination with the Flint library [4]. The final software library is expected to be presented in a wide audience journal such as ACM Transactions on Mathematical Software.