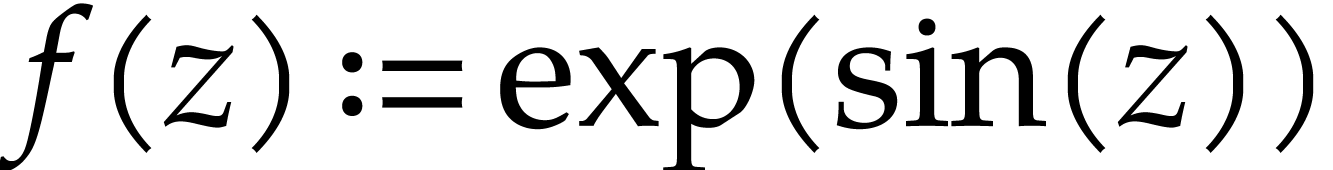 is the unique power series solution to the system of equations
is the unique power series solution to the system of equations 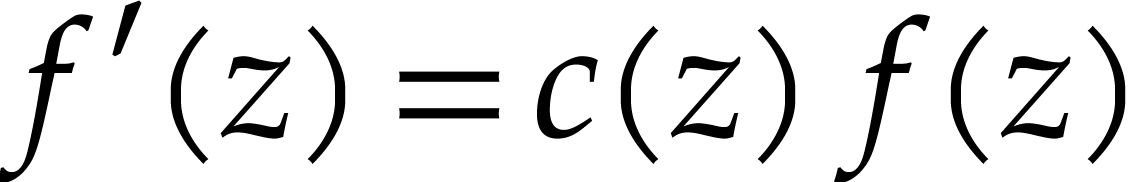 ,
, 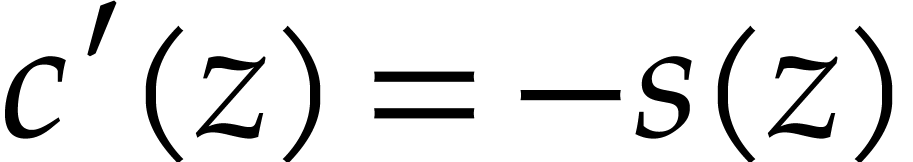 ,
,
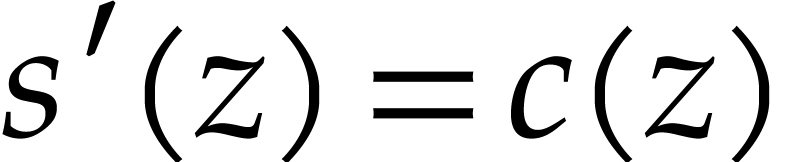 , with initial conditions
, with initial conditions
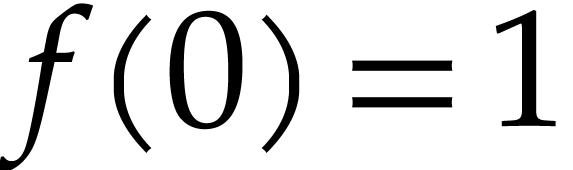 ,
, 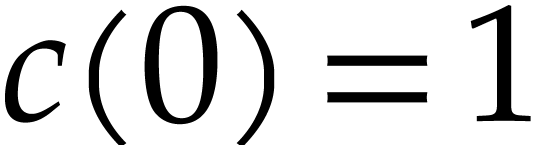 ,
, 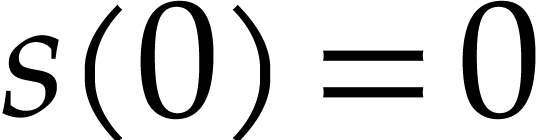 .
Assuming this kind of representation, how to check equalities like
.
Assuming this kind of representation, how to check equalities like 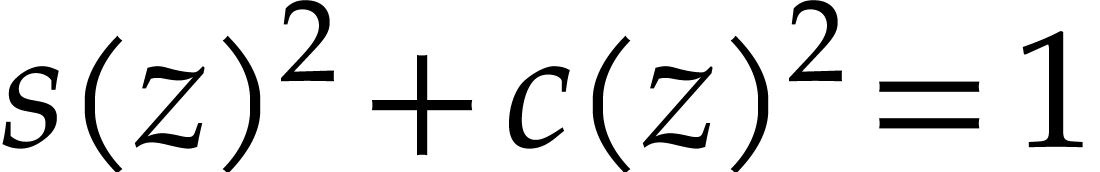 ?
?
ODELIX — PhD proposal |
| WelcomeTeamPublicationsSoftwareEventsJobsInternships |
Title: Computing transseries solutions to differential equations
Keywords: symbolic computation; automatic asymptotics; generalized series
Contact
Joris van der Hoeven <vdhoeven@lix.polytechnique.fr>
Address
Director of the laboratory: Mr Gilles Schaeffer <schaeffe@lix.polytechnique.fr>
Research team: MAX, Algebraic modeling and symbolic computation
Applying |
M2 students majoring in computer science or mathematics may apply. Basic familiarity with computer algebra is required. Knowledge about differential algebra is appreciated, but optional.
Applications should comprise a CV, a transcript of records, a letter of
motivation, and two recommendation letters. They should be sent to Joris
Description |
How to compute exactly and reliably with special functions in computer
algebra systems? One strategy is to adopt a local approach and
systematically represent such functions using power series around some
non-singular point. For instance, the function 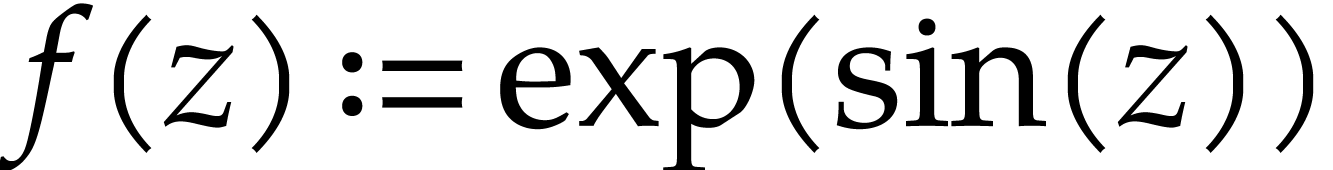 is the unique power series solution to the system of equations
is the unique power series solution to the system of equations 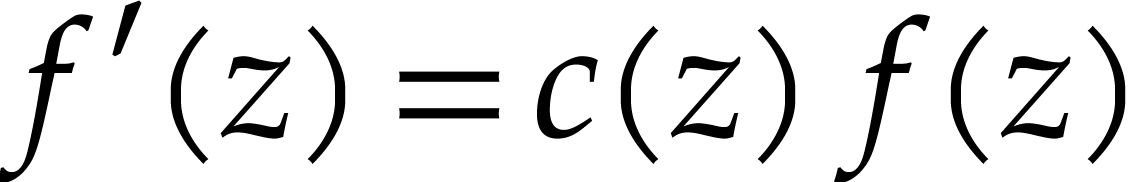 ,
, 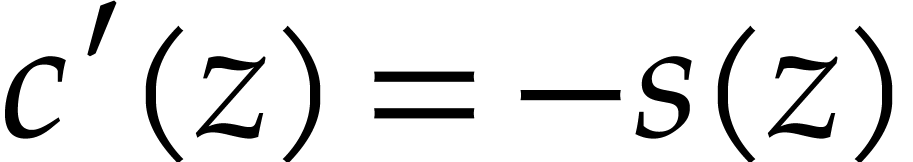 ,
,
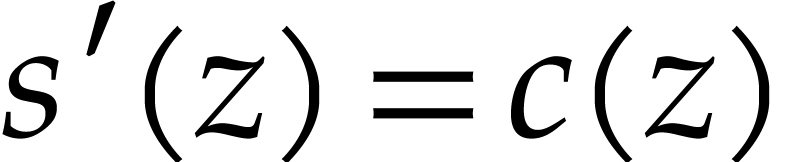 , with initial conditions
, with initial conditions
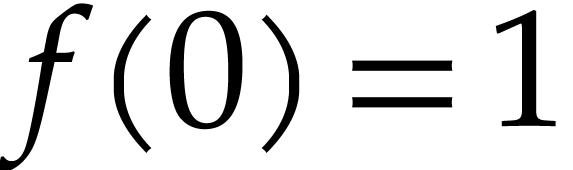 ,
, 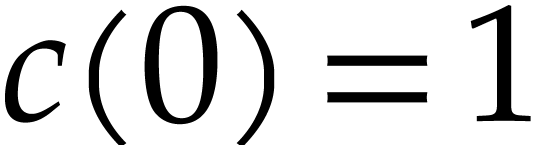 ,
, 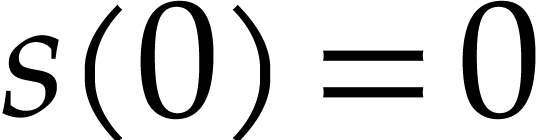 .
Assuming this kind of representation, how to check equalities like
.
Assuming this kind of representation, how to check equalities like 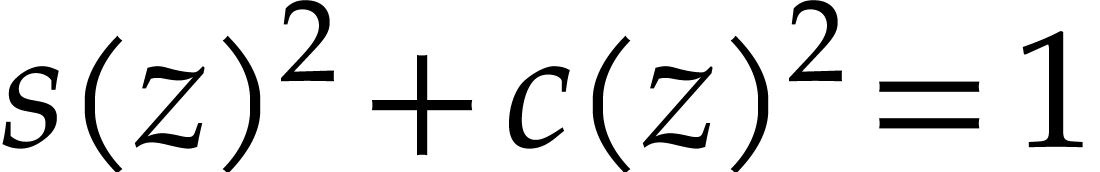 ?
?
Clearly, it suffices to have an algorithm for checking whether a given expression represent the zero function. When all power series are given as solutions of explicit differential equations with explicit initial conditions, several algorithms have been proposed for this zero test problem [2, 7, 6, 5]. One first challenge is to implement one or more of these algorithms and investigate possible improvements.
A second challenge concerns the computation of the generic power series
solution of a system of ordinary differential equations if the initial
conditions are not or only partially specified. This requires an
extension of the theory to the case when the coefficients of the power
series involve parameters. For instance, setting 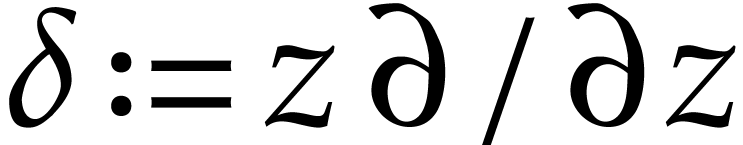 , the general solution to the equation
, the general solution to the equation 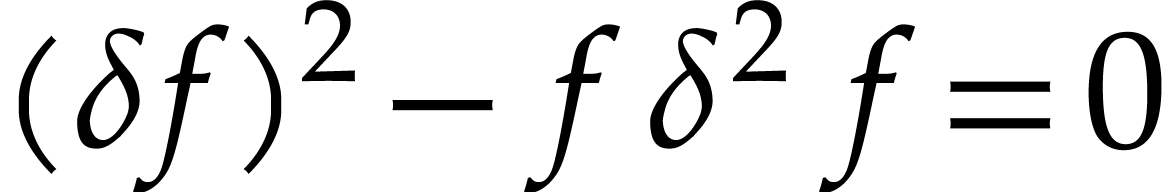 is
is 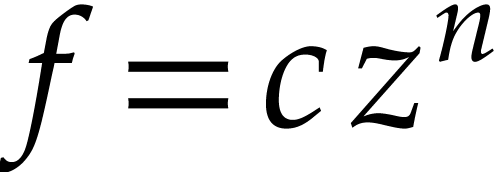 , where
, where 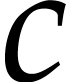 is an arbitrary constant and
is an arbitrary constant and  an arbitrary non-negative integer.
an arbitrary non-negative integer.
The main endgoal of the thesis is to further generalize this theory to
so-called transseries instead of ordinary power series [3,
4, 1]. A transseries is a generalized power
series that is allowed to recursively involve exponentials and
logarithms. For instance, 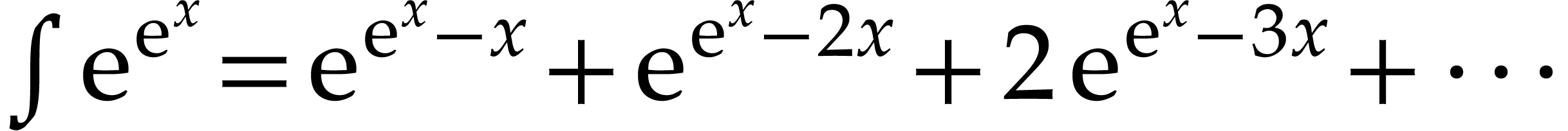 and
and 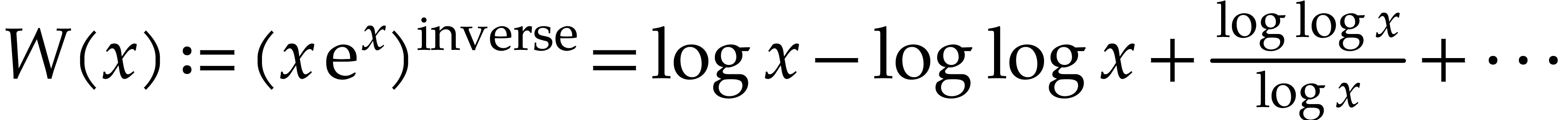 are transseries at infinity
are transseries at infinity  .
Transseries naturally arise when studying the asymptotic behavior of
solutions to ordinary differential equations. Ultimately, we would like
to have efficient zero tests for transseries and algorithms to find
transseries solutions of differential equations.
.
Transseries naturally arise when studying the asymptotic behavior of
solutions to ordinary differential equations. Ultimately, we would like
to have efficient zero tests for transseries and algorithms to find
transseries solutions of differential equations.
Methodology |
The thesis will start with a study of the existing literature. Next
increasingly difficult cases of zero testing and resolution of
differential equations will be considered. Depending on her or his
profile, the PhD student may choose to put greater emphasize on the
theoretical or practical aspects of the problem. Software
implementations will be open source and could done in
Expected results |
The theoretical part of the research should at least lead to a new zero test for differentially algebraic transseries. In addition, we hope that progress will be made on the computation of power series and transseries solutions to differential equations.
The algorithms will be tested at least on toy implementations. Depending on her or his profile, the PhD student may choose to develop a more advanced implementation that can be distributed as a library.
The new results should be published in prominent journals or conference proceedings of the area, such as JSC, AAECC, ISSAC, etc.
Bibliography |
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Asymptotic Differential Algebra and Model Theory of Transseries. Number 195 in Annals of Mathematics studies. Princeton University Press, 2017.
J. Denef and L. Lipshitz. Power series solutions of algebraic differential equations. Math. Ann., 267:213–238, 1984.
J. Écalle. Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac. Hermann, collection: Actualités mathématiques, 1992.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
J. van der Hoeven. Computing with D-algebraic power series. AAECC, 30(1):17–49, 2019.
A. Péladan-Germa. Tests effectifs de nullité dans des extensions d'anneaux différentiels. PhD thesis, Gage, École Polytechnique, Palaiseau, France, 1997.
J. Shackell. Zero equivalence in function fields defined by differential equations. Proc. of the AMS, 336(1):151–172, 1993.