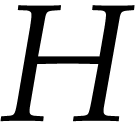 -fields aims at
studying the asymptotic behavior of such solutions from a formal
perspective.
-fields aims at
studying the asymptotic behavior of such solutions from a formal
perspective.
ODELIX — M2 internship proposal |
| WelcomeTeamPublicationsSoftwareEventsJobsInternships |
Title: Effective H-fields
Topics: automatic asymptotics, differential algebra, computer algebra
Address
Research team: MAX, Algebraic modeling and symbolic computation
Contact
Context
The MAX team is searching for PhD candidates on the themes of the “ODELIX” ERC Advanced Grant. The present M2 internship proposal allows applicants to familiarize themselves with these themes. Upon successful completion of the internship, there will be an opportunity to pursue with a PhD.
Applying
Applications can be sent by email to Joris
Description |
In a similar way as differential algebra was introduced in order to
study solutions of differential equations in a purely formal way, the
theory of 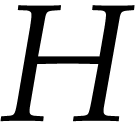 -fields aims at
studying the asymptotic behavior of such solutions from a formal
perspective.
-fields aims at
studying the asymptotic behavior of such solutions from a formal
perspective.
The language of 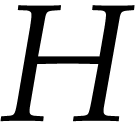 -fields
consists of the field operations
-fields
consists of the field operations 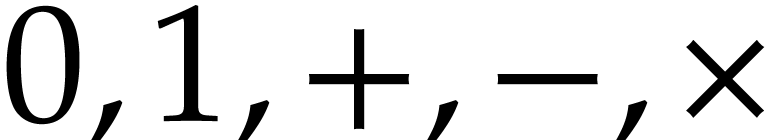 ,
differentiation
,
differentiation 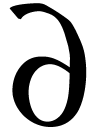 , and the
ordering
, and the
ordering  . The axioms for an
. The axioms for an
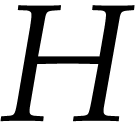 -field
-field  comprise the usual ordered field and differential fields axioms, as well
as two special axioms to express the compatability between the
derivation and the ordering: setting
comprise the usual ordered field and differential fields axioms, as well
as two special axioms to express the compatability between the
derivation and the ordering: setting 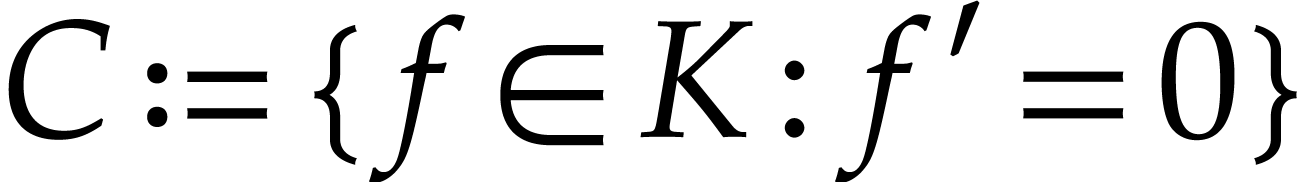 ,
,
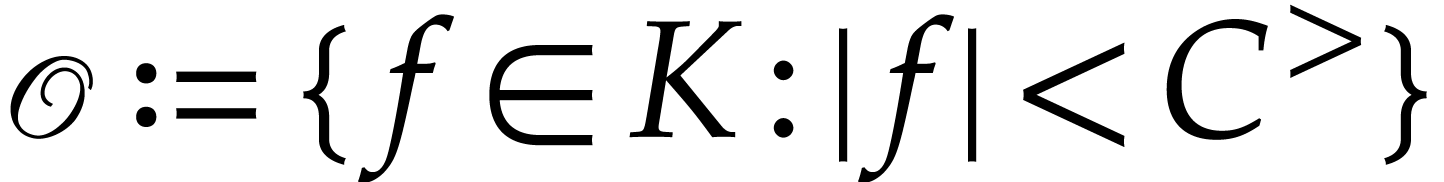 ,
, 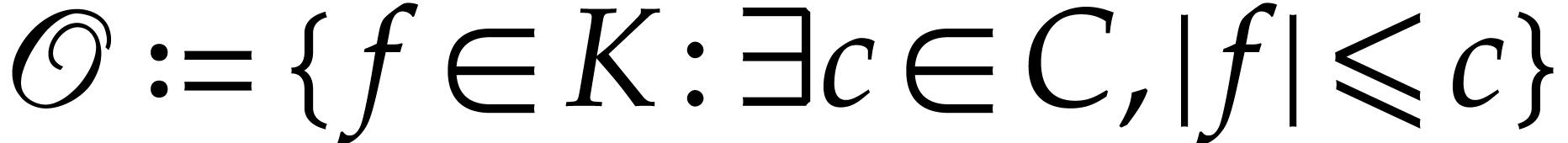 , we require that
, we require that  (for all
(for all
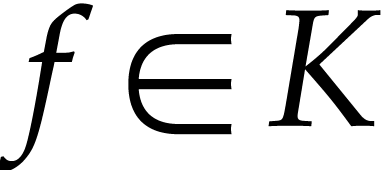 ) and
) and  .
.
The field of transseries  is a typical example of
an
is a typical example of
an  -field with a strong
algebraic flavor. A transseries [4, 7,
1] is a generalized power series that is allowed to
recursively involve exponentials and logarithms. For instance,
-field with a strong
algebraic flavor. A transseries [4, 7,
1] is a generalized power series that is allowed to
recursively involve exponentials and logarithms. For instance, 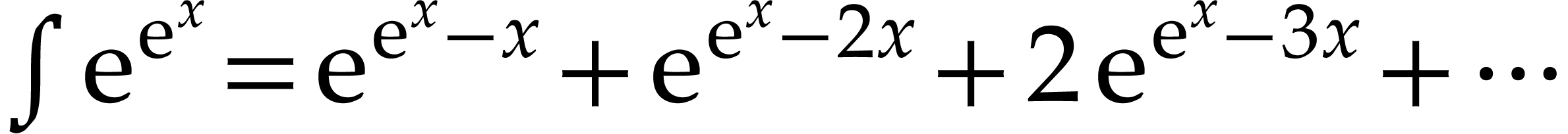 and
and 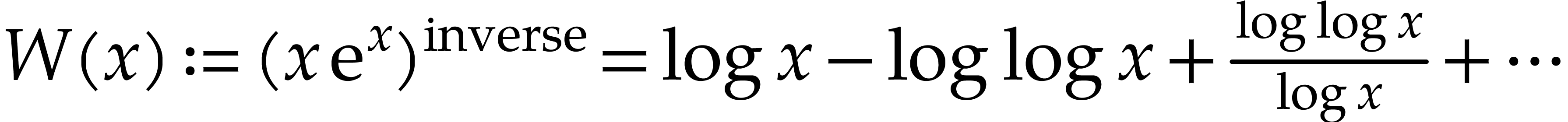 are transseries at infinity
are transseries at infinity
 . On the analytic side, any
Hardy field (e.g. a differential subfield of the
ring of germs of differentiable real functions at infinity [5,
6, 3, 2]) is an
. On the analytic side, any
Hardy field (e.g. a differential subfield of the
ring of germs of differentiable real functions at infinity [5,
6, 3, 2]) is an 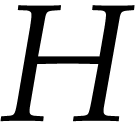 -field.
-field.
The ordering on an 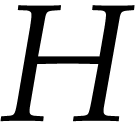 -field
-field
 naturally induces the asymptotic relations
naturally induces the asymptotic relations  and
and  defined by
defined by 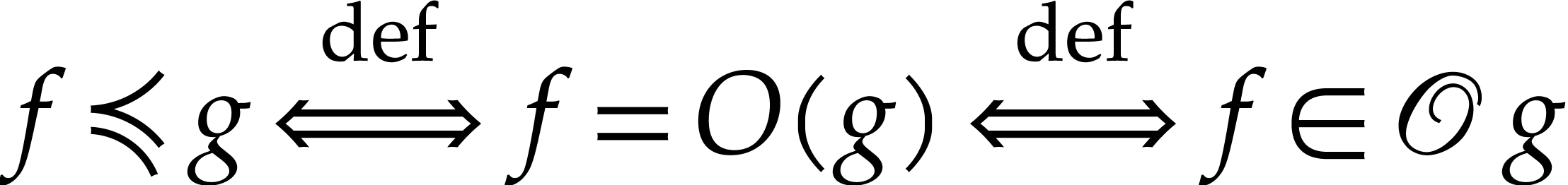 and
and 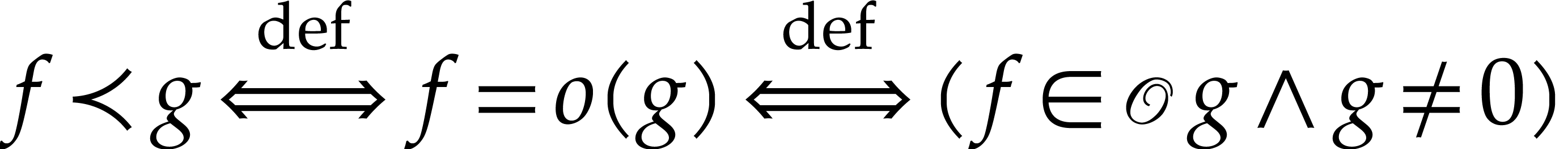 . For this
reason,
. For this
reason,  -fields are a
suitable framework for “asymptotic differential algebra” [1].
-fields are a
suitable framework for “asymptotic differential algebra” [1].
The aim of this internship is to develop an effective counterpart for
the theory of  -fields. Now
there exist various algorithms for asymptotic computations in specific
-fields. Now
there exist various algorithms for asymptotic computations in specific
 -fields like the field of
“exp-log” functions [8]. The idea here is to
develop this theory in a more abstract way. For this, we first define an
-fields like the field of
“exp-log” functions [8]. The idea here is to
develop this theory in a more abstract way. For this, we first define an
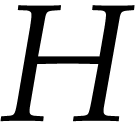 -field to be
effective if we can represent its elements on a computer and if
we have algorithms for the operations
-field to be
effective if we can represent its elements on a computer and if
we have algorithms for the operations 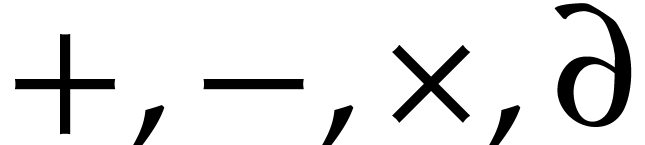 and for
the relations
and for
the relations  and
and  .
It is not hard to show that the real closure of an effective
.
It is not hard to show that the real closure of an effective 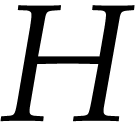 -field is again effective. The
internship will start with showing that we can also effectively close
under integration and exponentiation. After that, we will pursue with
the study of more complicated asymptotic differential equations.
-field is again effective. The
internship will start with showing that we can also effectively close
under integration and exponentiation. After that, we will pursue with
the study of more complicated asymptotic differential equations.
References |
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Asymptotic Differential Algebra and Model Theory of Transseries. Number 195 in Annals of Mathematics studies. Princeton University Press, 2017.
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Maximal Hardy Fields. Arxiv, 2023. https://arxiv.org/pdf/2304.10846.pdf.
N. Bourbaki. Fonctions d'une variable réelle. Éléments de Mathématiques (Chap. 5). Hermann, 2-nd edition, 1961.
J. Écalle. Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac. Hermann, collection: Actualités mathématiques, 1992.
G. H. Hardy. Orders of infinity. Cambridge Univ. Press, 1910.
G. H. Hardy. Properties of logarithmico-exponential functions. Proceedings of the London Mathematical Society, 10(2):54–90, 1911.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
D. Richardson, B. Salvy, J. Shackell, and J. van der Hoeven. Expansions of exp-log functions. In Proc. ISSAC '96, pages 309–313. Zürich, Switzerland, July 1996.