 matrices,
the product of two polynomials of degree
matrices,
the product of two polynomials of degree 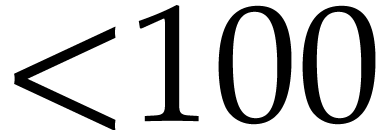 ,
a discrete Fourier transform (DFT) of length
,
a discrete Fourier transform (DFT) of length 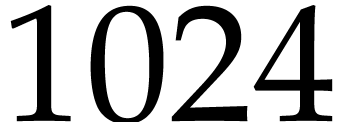 [6], arithmetic operations on medium precision numerical types
[4], or ball arithmetic over such types [8, 5].
[6], arithmetic operations on medium precision numerical types
[4], or ball arithmetic over such types [8, 5].
ODELIX — M2 internship proposal |
| WelcomeTeamPublicationsSoftwareEventsJobsInternships |
Title: SIMD acceleration of straight-line programs
Topics: symbolic and numeric algorithms, parallelism, complexity
Address
Research team: MAX, Algebraic modeling and symbolic computation
Contacts
Context
The MAX team is searching for PhD candidates on the themes of the “ODELIX” ERC Advanced Grant. The present M2 internship proposal allows applicants to familiarize themselves with these themes. Upon successful completion of the internship, there will be an opportunity to pursue with a PhD.
Applying
Applications can be sent by email to the above contact persons; they
should include a CV, a transcript of records, a letter of motivation,
and optional recommendation letters. Note that we have no hard
deadlines; new applications will be considered at any time of the year,
as long as the
Description |
Elementary arithmetic operations such as additions and multiplications of integers, polynomials, and series are usually described and implemented in a sequential calculation model [2, 3, 1]. This project proposes to study algorithmic variants which take advantage of SIMD (Single Instruction Multiple Data) parallelism inside modern CPUs. SIMD instructions perform operations on vectors of machine integers or floating point numbers instead. In very favorable situations, one expects a speedup with respect to the scalar (non-SIMD) version that corresponds to the width of the vectors. For instance, on a CPU with AVX512 support, the maximal vector length is eight for double precision numbers and sixteen in single precision.
Transforming a general program into one that exploits SIMD accelerations
is a difficult task that is typically carried out only imperfectly by
the compiler. For the present internship, we will restrict our attention
to a very simple type of so-called straight-line programs (SLPs) that
only perform very simple arithmetic instructions and no branching. Many
interesting operations on objects of a fixed size can be carried out
using SLPs, such as the product of two  matrices,
the product of two polynomials of degree
matrices,
the product of two polynomials of degree 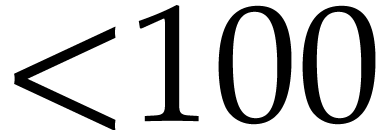 ,
a discrete Fourier transform (DFT) of length
,
a discrete Fourier transform (DFT) of length 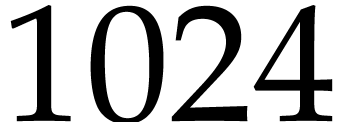 [6], arithmetic operations on medium precision numerical types
[4], or ball arithmetic over such types [8, 5].
[6], arithmetic operations on medium precision numerical types
[4], or ball arithmetic over such types [8, 5].
The main goal of the internship is to study how SLPs can benefit from
SIMD accelerations. Ideally speaking, one might try to find an optimal
SIMD SLP for computing the same result. However, the SLPs that we are
interested in typically become very large, which makes it hard to
compute such optimal accelerators. Instead we will focus on common SLPs
encountered in computer algebra and computer arithmetic, like the above
examples. The hope is to generate almost optimal SIMD accelerators for
such SLPs in a semi-automatic fashion. For instance, a first question
might be the generation of a SIMD SLP for the product of an 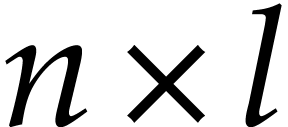 and an
and an 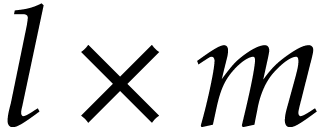 matrix product. Here
matrix product. Here 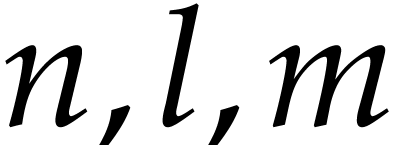 are parameters, but the programmer knows how to
exploit the particular mathematical structure behind matrix products.
are parameters, but the programmer knows how to
exploit the particular mathematical structure behind matrix products.
Implementations will be released under an open source software license
and the student will be able to test them on Apple Silicon, Intel Xeon,
and AMD Zen CPUs. Ultimately, we hope to integrate this type of
functionality in the
We seek for excellent candidates with a background in computer science. Applicants will be required to have knowledge in algorithms, parallelism, high performance computing and complexity. Programming skills will be useful to achieve efficient implementations.
References |
A. Bostan, F. Chyzak, M. Giusti, R. Lebreton, G. Lecerf, B. Salvy, and É. Schost. Algorithmes Efficaces en Calcul Formel. Frédéric Chyzak (self-published), Palaiseau, 2017. Electronic version available from https://hal.archives-ouvertes.fr/AECF.
R. P. Brent and P. Zimmermann. Modern Computer Arithmetic. Cambridge University Press, 2010.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, New York, NY, USA, 3rd edition, 2013.
J. van der Hoeven and G. Lecerf. Faster FFTs in medium precision. In 22nd IEEE Symposium on Computer Arithmetic (ARITH), pages 75–82. June 2015.
J. van der Hoeven and G. Lecerf. Evaluating straight-line programs over balls. In 23nd IEEE Symposium on Computer Arithmetic (ARITH), pages 142–149. 2016.
J. van der Hoeven and G. Lecerf. Implementing number theoretic transforms. Technical Report, HAL, 2024. https://hal.science/hal-04841449.
J. van der Hoeven, G. Lecerf, B. Mourain, Ph. Trébuchet, J. Berthomieu, D. Diatta, and A. Mantzaflaris. Mathemagix, the quest of modularity and efficiency for symbolic and certified numeric computation. ACM SIGSAM Communications in Computer Algebra, 177(3), 2011. In Section "ISSAC 2011 Software Demonstrations", edited by M. Stillman, p. 166–188.
J. van der Hoeven, G. Lecerf, and G. Quintin. Modular SIMD arithmetic in Mathemagix. ACM Trans. Math. Softw., 43(1):5–1, 2016.
G. Lecerf. New recombination algorithms for bivariate polynomial factorization based on Hensel lifting. AAECC, 21(2):151–176, 2010.