Title: Numeric-symbolic polynomial system
solving
Topics: symbolic and numeric algorithms, polynomial
system solving, complexity
Address
1 rue Honoré d'Estienne d'Orves
91120 Palaiseau, France
Research team: MAX, Algebraic modeling and symbolic
computation
Contacts
Context
The MAX team is searching for PhD candidates on the themes of the
“ODELIX” ERC Advanced Grant. The present M2 internship
proposal allows applicants to familiarize themselves with these themes.
Upon successful completion of the internship, there will be an
opportunity to pursue with a PhD.
Applying
Applications can be sent by email to the above contact persons; they
should include a CV, a transcript of records, a letter of motivation,
and optional recommendation letters. Note that we have no hard
deadlines; new applications will be considered at any time of the year,
as long as the Odelix project runs.
The resolution of algebraic systems is a flagship tool for computer
algebra, with many applications in robotics, chemistry, signal,
cryptology, etc. The complexity bounds have been mostly studied in worst
cases, and they turn out to be often very pessimistic. It is therefore
necessary, for a given problem, to take advantage of its specific
features.
For rational number coefficient systems, the numeric methods behave well
in practice for sufficiently generic input systems, and have been a very
active research topic for fifty years. Popular methods proceed by
deformations. First, one chooses a system of a geometric nature close to
the system to be solved and from which one can determine solutions
quickly. Then, one deforms the system so that be able to update
solutions efficiently and finally arrive at those of the input system.
In the numeric framework, certifying the solution set is a tedious
problem. At least certifying regular isolated solutions turns out to be
rather easy and efficient in practice.
This internship will focus on the certification of solutions that are
not necessarily isolated or regular. A first objective will be to deepen
the knowledge of algebraic geometry and numerical calculation necessary
for understanding algorithms by deformation [1, 7,
6]. The second objective will concern practical tools used
to certify numeric calculations. One popular approach to reliable
computation is to use interval or ball arithmetic [3, 5, 4]. This amounts to systematically replace any
floating point approximation 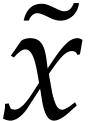 of a real number
of a real number
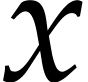 by an interval
by an interval 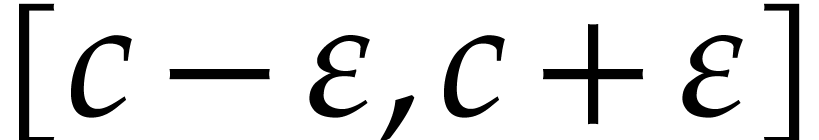 that is
certified to contain the exact value
that is
certified to contain the exact value 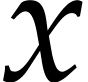 .
Then, the main part of the internship will concern comparisons of
certification algorithms of solutions [2, 8,
9]. The algorithms will be implemented in the Mathemagix
framework (http://www.mathemagix.org),
that already contains the necessary basic data structures (balls,
polynomials, series, matrices).
.
Then, the main part of the internship will concern comparisons of
certification algorithms of solutions [2, 8,
9]. The algorithms will be implemented in the Mathemagix
framework (http://www.mathemagix.org),
that already contains the necessary basic data structures (balls,
polynomials, series, matrices).
We seek for excellent candidates with a background both in mathematics
and computer science. Applicants will be required to have knowledge in
algebra, algorithms, and complexity. Programming skills will be useful
to achieve efficient implementations.
-
[1]
-
A. Bostan, F. Chyzak, M. Giusti, R. Lebreton, G.
Lecerf, B. Salvy, and É. Schost. Algorithmes Efficaces
en Calcul Formel. Frédéric Chyzak
(auto-édit.), Palaiseau, 2017. 686 pages. Imprimé
par CreateSpace. Aussi disponible en version électronique
à https://hal.archives-ouvertes.fr/AECF.
-
[2]
-
J. van der Hoeven. On effective analytic continuation.
Mathematics in Computer Science, 1(1):111–175, 2007.
-
[3]
-
J. van der Hoeven. Ball arithmetic. Technical Report,
HAL, 2009. https://hal.archives-ouvertes.fr/hal-00432152.
-
[4]
-
J. van der Hoeven. Journées Nationales de
Calcul Formel (2011), volume 2 of Les cours du CIRM,
chapter Calcul analytique. CEDRAM, 2011. Exp. No. 4, 85 pages, http://ccirm.cedram.org/ccirm-bin/fitem?id=CCIRM_2011__2_1_A4_0.
-
[5]
-
J. van der Hoeven and G. Lecerf. Evaluating
straight-line programs over balls. In P. Montuschi, M. Schulte, J.
Hormigo, S. Oberman, and N. Revol, editors, 2016 IEEE 23nd
Symposium on Computer Arithmetic, pages 142–149. IEEE,
2016.
-
[6]
-
J. van der Hoeven and G. Lecerf. On the complexity
exponent of polynomial system solving. Found. Comput.
Math., 21:1–57, 2021.
-
[7]
-
G. Lecerf. Computing an equidimensional decomposition
of an algebraic variety by means of geometric resolutions. In C.
Traverso, editor, Proc. ISSAC '00, pages 209–216.
ACM, 2000.
-
[8]
-
Angelos Mantzaflaris, Bernard Mourrain, and Agnes
Szanto. A certified iterative method for isolated singular roots.
Journal of Symbolic Computation, 115:223–247, 2023.
-
[9]
-
Simon Telen, Marc Van Barel, and Jan Verschelde. A
robust numerical path tracking algorithm for polynomial homotopy
continuation. SIAM Journal on Scientific Computing, 42(6),
2020.
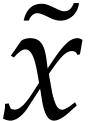 of a real number
of a real number
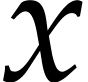 by an interval
by an interval 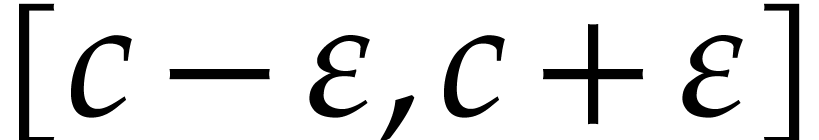 that is
certified to contain the exact value
that is
certified to contain the exact value 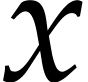 .
Then, the main part of the internship will concern comparisons of
certification algorithms of solutions [2, 8,
9]. The algorithms will be implemented in the
.
Then, the main part of the internship will concern comparisons of
certification algorithms of solutions [2, 8,
9]. The algorithms will be implemented in the