Title: Fast evaluation of elementary functions with
medium precision
Topics: reliable numerical algorithms, high performance
computing
Address
1 rue Honoré d'Estienne d'Orves
91120 Palaiseau, France
Research team: MAX, Algebraic modeling and symbolic
computation
Contacts
Context
The MAX team is searching for PhD candidates on the themes of the
“ODELIX” ERC Advanced Grant. The present M2 internship
proposal allows applicants to familiarize themselves with these themes.
Upon successful completion of the internship, there will be an
opportunity to pursue with a PhD.
Applying
Applications can be sent by email to the above contact persons; they
should include a CV, a transcript of records, a letter of motivation,
and optional recommendation letters. Note that we have no hard
deadlines; new applications will be considered at any time of the year,
as long as the Odelix project runs.
The class of elementary functions consists of the exponential,
the trigonometric functions  ,
,
 ,
,  , the hyperbolic functions
, the hyperbolic functions  ,
,  ,
,  , and their functional inverses
, and their functional inverses
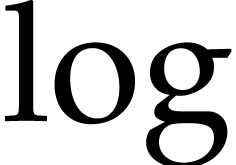 ,
,  ,
,  ,
,  ,
, 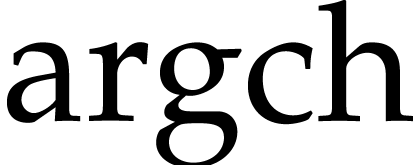 ,
,
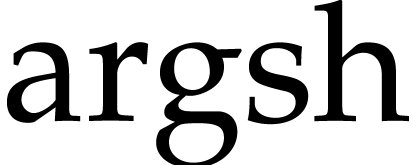 , and
, and 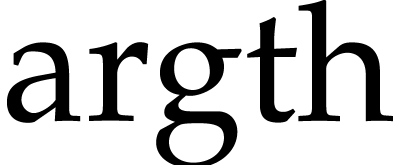 . In C and C++, these functions are in the standard
libm library. This implementation is highly optimized,
but limited to single (24 bits) and double (53 bits) precisions. On the
other side of the spectrum, dedicated libraries such as Mpfr
[1] can be used to evaluate elementary functions
efficiently with very large precisions. In the context of modern
safety-critical applications such as aerospace engineering and
autonomous vehicles design, computing with precision higher than the
standard ones is required but the full power of Mpfr
may be an overkill.
. In C and C++, these functions are in the standard
libm library. This implementation is highly optimized,
but limited to single (24 bits) and double (53 bits) precisions. On the
other side of the spectrum, dedicated libraries such as Mpfr
[1] can be used to evaluate elementary functions
efficiently with very large precisions. In the context of modern
safety-critical applications such as aerospace engineering and
autonomous vehicles design, computing with precision higher than the
standard ones is required but the full power of Mpfr
may be an overkill.
The aim of this internship is to produce a highly optimized
implementation for “medium precisions” until 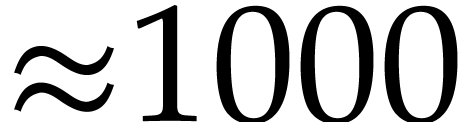 bits. This raises several interesting challenges:
bits. This raises several interesting challenges:
-
How to represent medium precision floating point numbers?
-
How to exploit SIMD (single instruction multiple data) instructions
in modern processors to speed-up evaluations by an appreciable
constant factor.
-
How to exploit special properties of elementary functions for the
design of efficient implementations for each of the target
precisions?
-
How to guarantee the correctness of the algorithms modulo rounding
errors?
For the first two items, one may use and further extend techniques that
were developed in [3, 2]. The goal is to
produce a C or C++ library that can reliably evaluate elementary
functions for any medium precision; see also [4].
Optionally, one may examine the generalization of the methods to other
special functions. Of particular interest in this respect is the class
of holonomic functions, i.e. functions 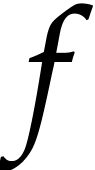 that satisfy a non-trivial linear differential equation
that satisfy a non-trivial linear differential equation
 for polynomials
for polynomials 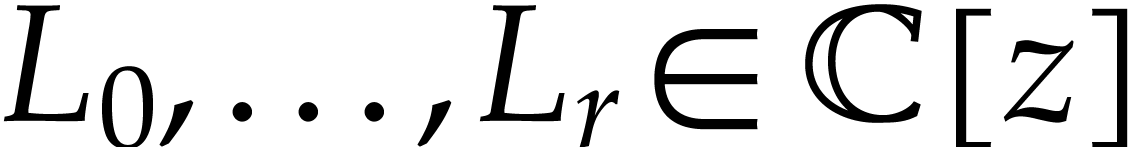 .
In [5], a library is described that allows to efficiently
and reliably evaluate such functions with high precision. It would be
interesting to have a similar library for medium precisions.
.
In [5], a library is described that allows to efficiently
and reliably evaluate such functions with high precision. It would be
interesting to have a similar library for medium precisions.
-
[1]
-
G. Hanrot, V. Lefèvre, K. Ryde, and P.
Zimmermann. MPFR, a C library for multiple-precision
floating-point computations with exact rounding. http://www.mpfr.org,
2000.
-
[2]
-
J. van der Hoeven. Multiple precision floating-point
arithmetic on SIMD processors. In N. Burgess, J. D. Bruguera, and
F. de Dinechin, editors, 24th Symposium on Computer Arithmetic
(ARITH), pages 2–9. July 2017.
-
[3]
-
J. van der Hoeven and G. Lecerf. Faster FFTs in medium
precision. In 22nd Symposium on Computer Arithmetic
(ARITH), pages 75–82. June 2015.
-
[4]
-
F. Johansson. Efficient implementation of elementary
functions in the medium-precision range. In 2015 IEEE 22nd
Symposium on Computer Arithmetic, pages 83–89. 2015.
-
[5]
-
M. Mezzarobba. Rigorous multiple-precision evaluation
of D-Finite functions in SageMath. Technical Report, HAL, 2016. https://hal.archives-ouvertes.fr/hal-01342769.
 ,
,
 ,
,  , the hyperbolic functions
, the hyperbolic functions  ,
,  ,
,  , and their functional inverses
, and their functional inverses
 ,
,  ,
,  ,
,  ,
, 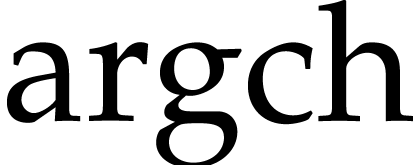 ,
,
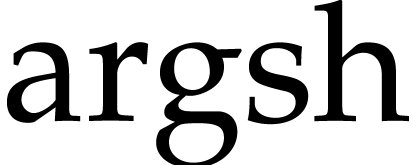 , and
, and 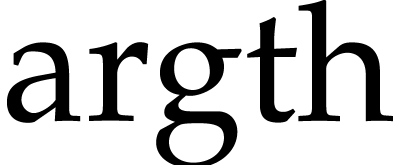 . In C and C++, these functions are in the standard
libm library. This implementation is highly optimized,
but limited to single (24 bits) and double (53 bits) precisions. On the
other side of the spectrum, dedicated libraries such as
. In C and C++, these functions are in the standard
libm library. This implementation is highly optimized,
but limited to single (24 bits) and double (53 bits) precisions. On the
other side of the spectrum, dedicated libraries such as 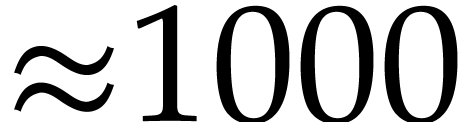 bits. This raises several interesting challenges:
bits. This raises several interesting challenges:
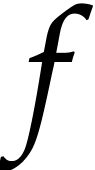 that satisfy a non-trivial linear differential equation
that satisfy a non-trivial linear differential equation
 for polynomials
for polynomials 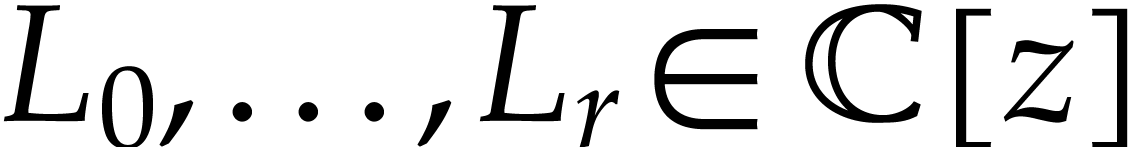 .
.