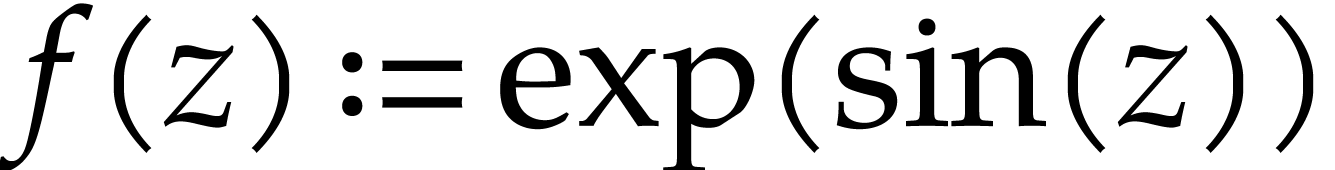 is the unique power series solution to the system of equations
is the unique power series solution to the system of equations 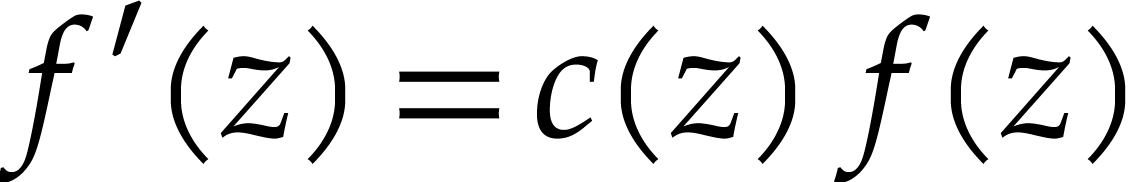 ,
, 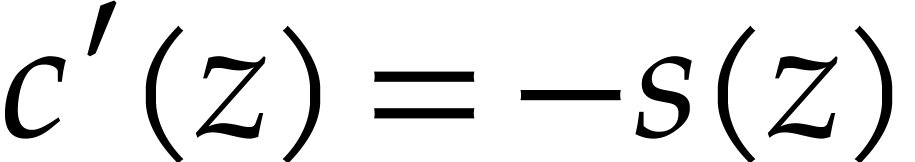 ,
,
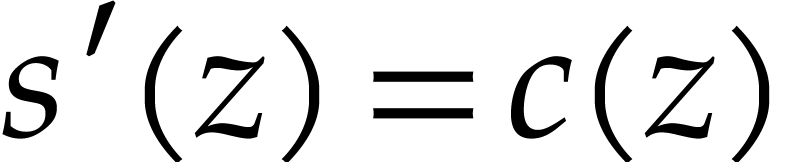 , with initial conditions
, with initial conditions
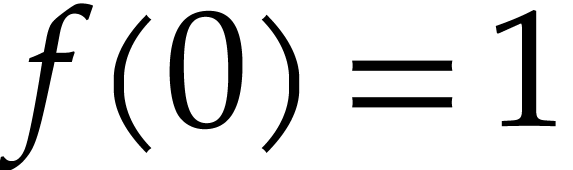 ,
, 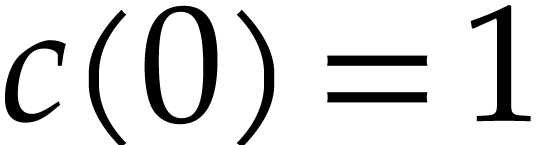 ,
, 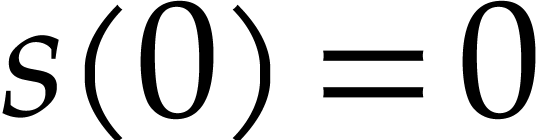 .
Assuming this kind of representation, how to check equalities like
.
Assuming this kind of representation, how to check equalities like 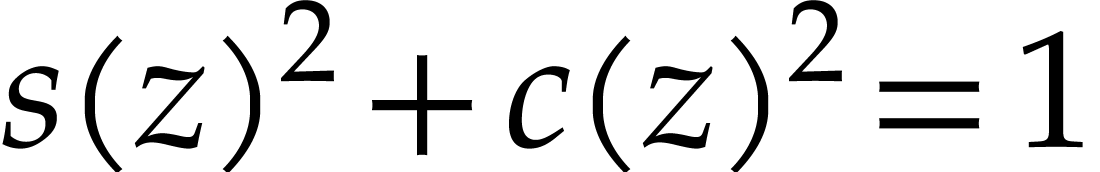 ?
?
ODELIX — M2 internship proposal |
| WelcomeTeamPublicationsSoftwareEventsJobsInternships |
Title: Zero-testing for differentially algebraic transseries
Topics: automatic asymptotics, differential algebra, computer algebra
Address
Research team: MAX, Algebraic modeling and symbolic computation
Contacts
Context
The MAX team is searching for PhD candidates on the themes of the “ODELIX” ERC Advanced Grant. The present M2 internship proposal allows applicants to familiarize themselves with these themes. Upon successful completion of the internship, there will be an opportunity to pursue with a PhD.
Applying
Applications can be sent by email to the above contact persons; they
should include a CV, a transcript of records, a letter of motivation,
and optional recommendation letters. Note that we have no hard
deadlines; new applications will be considered at any time of the year,
as long as the
Description |
How to compute exactly and reliably with special functions in computer
algebra systems? One strategy is to adopt a local approach and
systematically represent such functions using power series around some
non-singular point. For instance, the function 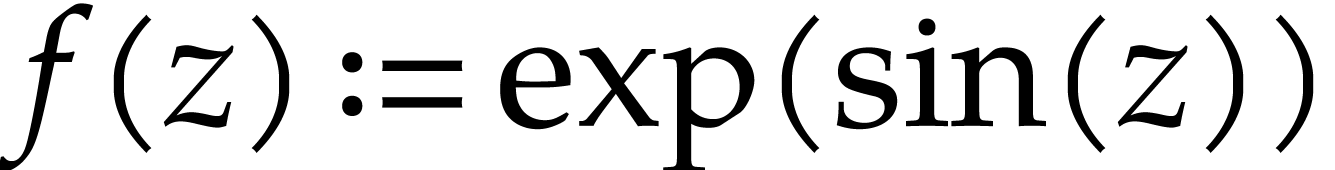 is the unique power series solution to the system of equations
is the unique power series solution to the system of equations 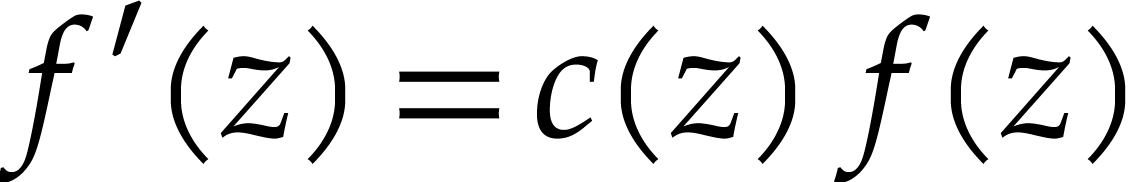 ,
, 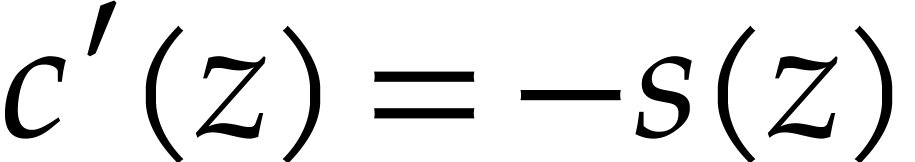 ,
,
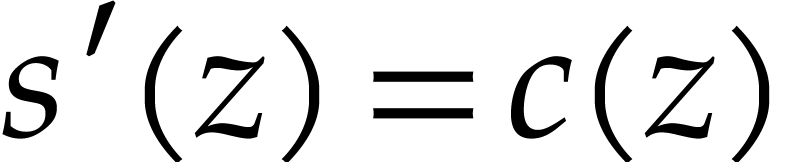 , with initial conditions
, with initial conditions
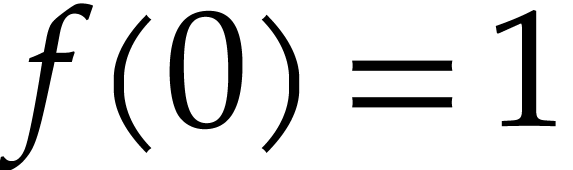 ,
, 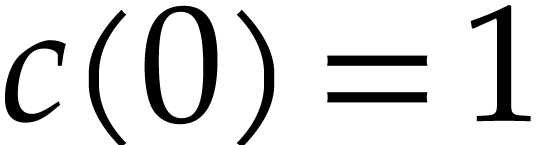 ,
, 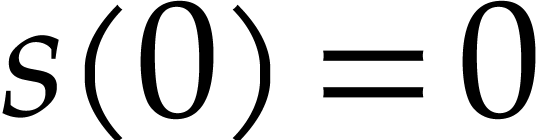 .
Assuming this kind of representation, how to check equalities like
.
Assuming this kind of representation, how to check equalities like 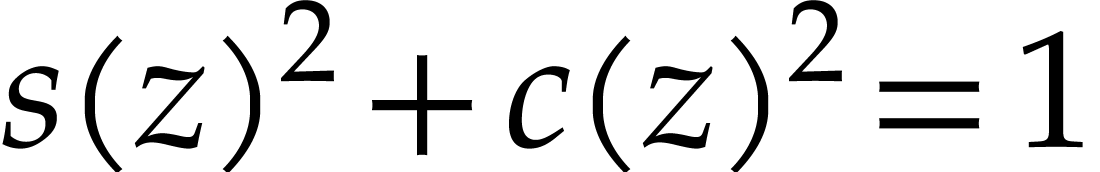 ?
?
Clearly, it suffices to have an algorithm for checking whether a given expression represent the zero function. When all power series are given as solutions of explicit differential equations with explicit initial conditions, several algorithms have been proposed for this zero test problem [2, 7, 6, 5]. One first challenge is to implement one or more of these algorithms and investigate possible improvements.
The aim of this internship is to generalize these algorithms to
expressions that represent so-called transseries instead of ordinary
power series [3, 4, 1]. A
transseries is a generalized power series that is allowed to
recursively involve exponentials and logarithms. For instance, 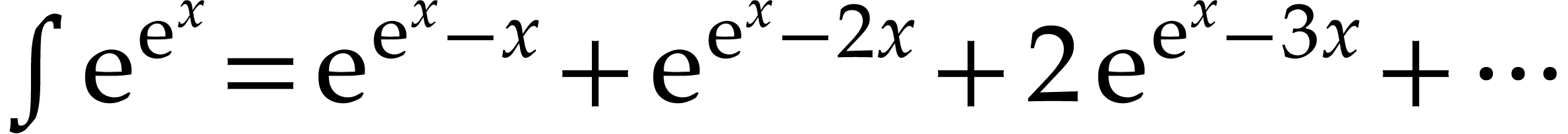 and
and 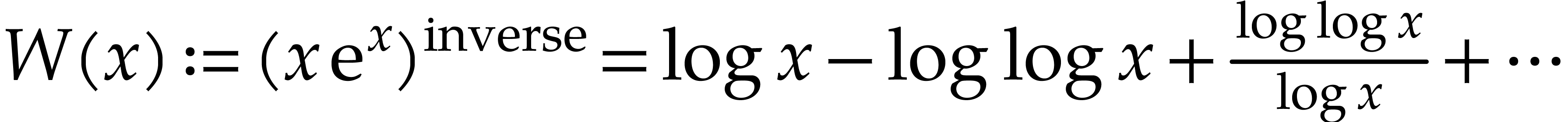 are transseries at infinity
are transseries at infinity
 . Transseries naturally arise
when studying the asymptotic behavior of solutions to ordinary
differential equations.
. Transseries naturally arise
when studying the asymptotic behavior of solutions to ordinary
differential equations.
We seek for excellent candidates with a background in mathematics and with an appetite for programming and making mathematical theory more effective.
References |
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Asymptotic Differential Algebra and Model Theory of Transseries. Number 195 in Annals of Mathematics studies. Princeton University Press, 2017.
J. Denef and L. Lipshitz. Power series solutions of algebraic differential equations. Math. Ann., 267:213–238, 1984.
J. Écalle. Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac. Hermann, collection: Actualités mathématiques, 1992.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
J. van der Hoeven. Computing with D-algebraic power series. AAECC, 30(1):17–49, 2019.
A. Péladan-Germa. Tests effectifs de nullité dans des extensions d'anneaux différentiels. PhD thesis, Gage, École Polytechnique, Palaiseau, France, 1997.
J. Shackell. Zero equivalence in function fields defined by differential equations. Proc. of the AMS, 336(1):151–172, 1993.