 |
Efficient reliable symbolic-numeric integrators |  |
PhD proposal 2024–2027
Title: Efficient reliable symbolic-numeric integrators
Keywords: symbolic and numeric algorithms; reliable computing; integrators
Contacts
Applying
Applications should comprise a CV, a transcript of records, a letter of motivation, and optional recommendation letters. They should be sent to Joris van der Hoeven before April 15, 2024.
Address
Director of the laboratory: Mr Gilles Schaeffer (schaeffe@lix.polytechnique.fr)
Research team: MAX, Algebraic modeling and symbolic computation
M2 students majoring in computer science or mathematics may apply. Knowledge in at least one of the following topics is required: complexity theory, fast elementary algorithms, differential calculus, high performance computing.
Description
How to predict planetary motion, the spread of an epidemic, or the evolution of a chemical reaction network? Here are some of the many problems that can be modeled by ordinary differential equations (ODEs). The resolution of such equations has a long history and remains an important problem in science and technology.
A system of ordinary differential equations is given in the form
 |
(1) |
where 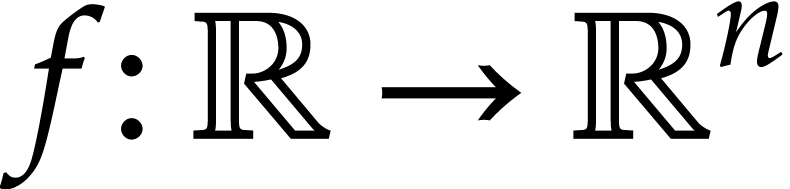 is an unknown function and
is an unknown function and 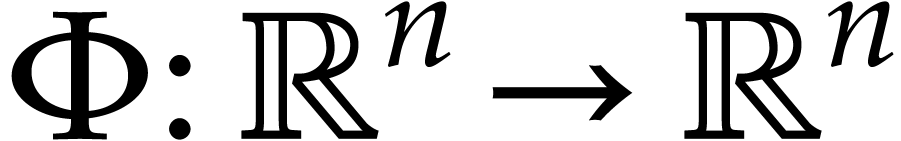 represents the actual equations. Given a
represents the actual equations. Given a 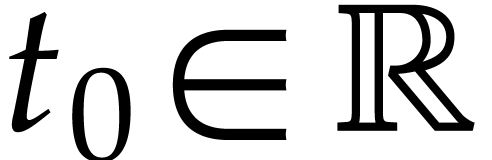 and an initial condition
and an initial condition 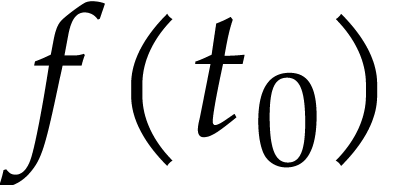 ,
the resolution problem consists in computing the value of
,
the resolution problem consists in computing the value of 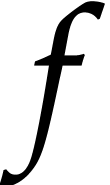 at a given point
at a given point 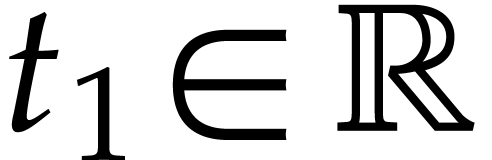 .
.
If  has specific properties, then the solution
has specific properties, then the solution
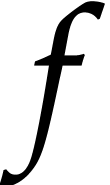 has a closed symbolic form: for instance if
has a closed symbolic form: for instance if
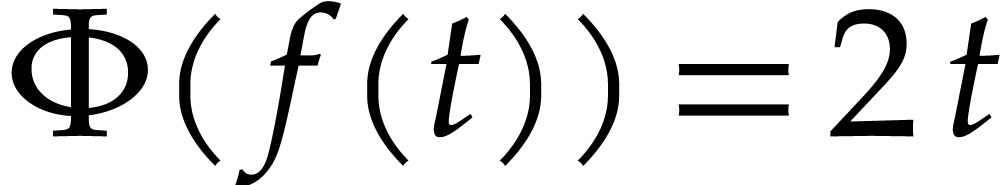 ,
, 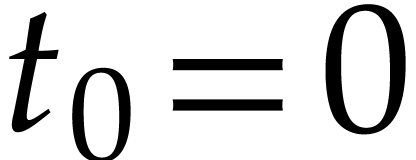 , and
, and 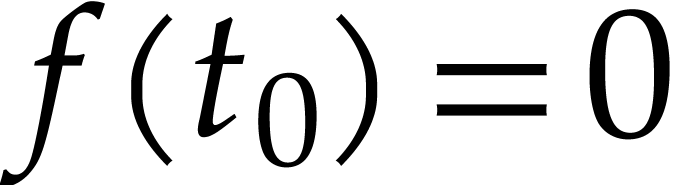 ,
then the solution is
,
then the solution is 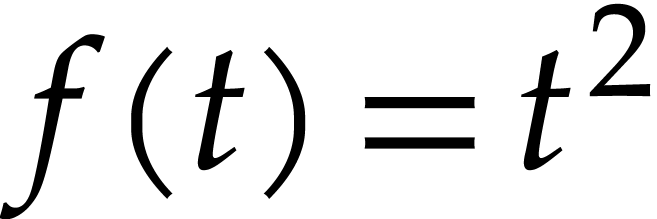 . In general such closed
forms do not exist and numerical integration algorithms are used for
computing approximations of the values of
. In general such closed
forms do not exist and numerical integration algorithms are used for
computing approximations of the values of 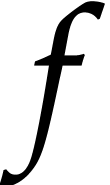 .
.
Numerical integrators compute a sequence of approximations  , where
, where  and the steps
and the steps
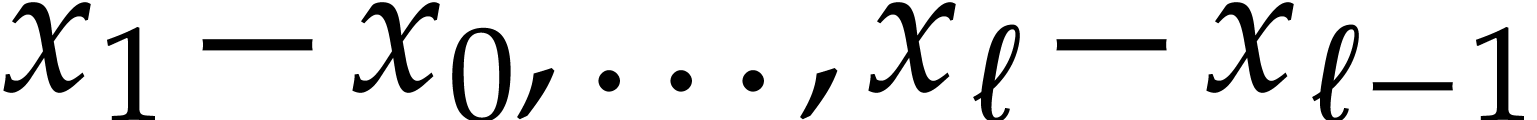 are small. For
are small. For  , we may
compute
, we may
compute 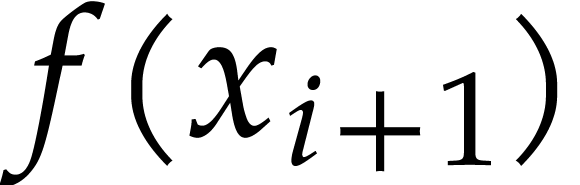 from
from 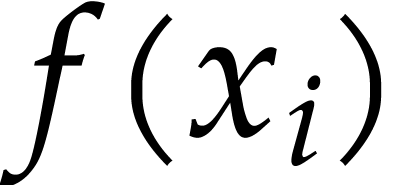 by
rewriting (1) into
by
rewriting (1) into
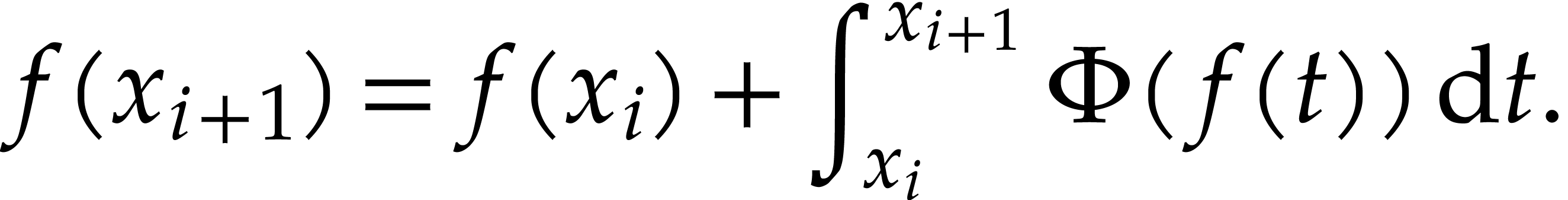
Runge–Kutta schemes are a popular way to approximate the above
integrals. For a method of order 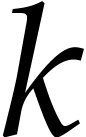 , the
error of
, the
error of 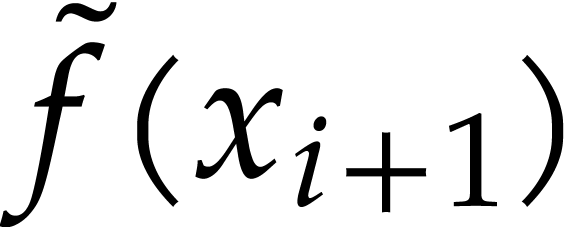 is bounded by
is bounded by 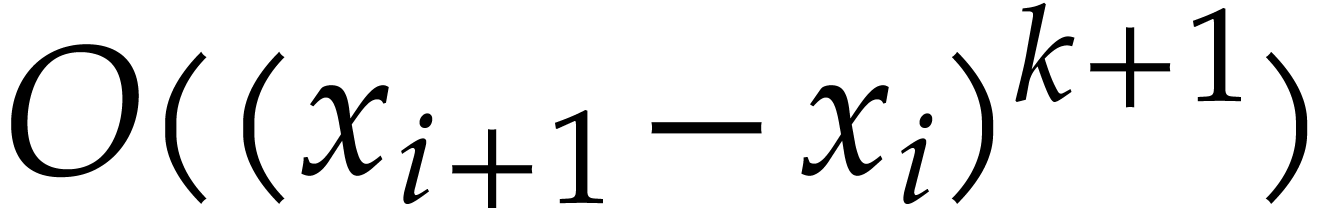 .
.
A numeric integrator for  , it can automatically produce an approximation
, it can automatically produce an approximation
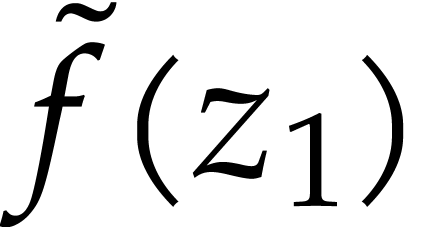 of
of 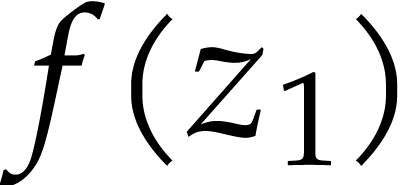 with
with 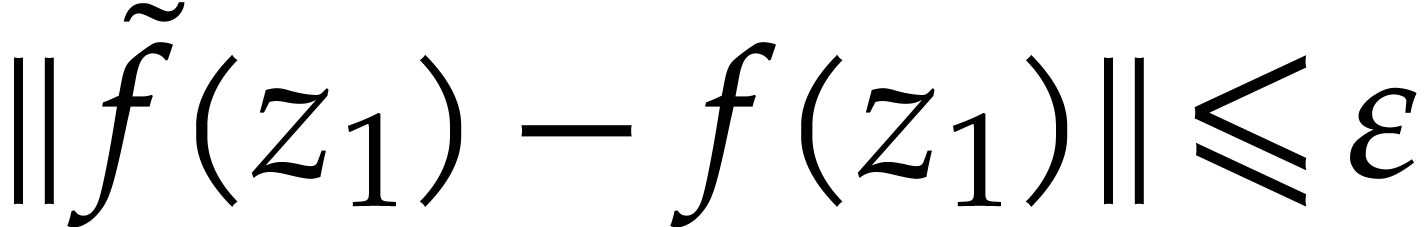 , when it exists. Current implementations of numerical
integrators are not of this type and extensive simulations are
required to verify the soundness of the computed results. However,
simulations can only test a finite number of examples and types of
incidents; severe accidents may and indeed do happen in exceptional
cases that were not covered. Enriching numerical software with
automatic tools to guarantee the correctness is a major and necessary
step forward to avoid such accidents.
, when it exists. Current implementations of numerical
integrators are not of this type and extensive simulations are
required to verify the soundness of the computed results. However,
simulations can only test a finite number of examples and types of
incidents; severe accidents may and indeed do happen in exceptional
cases that were not covered. Enriching numerical software with
automatic tools to guarantee the correctness is a major and necessary
step forward to avoid such accidents.
This PhD thesis concerns the design, analysis, and software implementation of a new efficient reliable integrator. Depending on her or his profile, the PhD student may chose to put greater emphasis on the theoretical or practical aspects of the problem.
Context
The numeric integration of systems of differential equations like
 is usually smooth and the integration
is typically done with machine precision (
is usually smooth and the integration
is typically done with machine precision (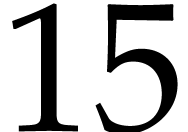 digits after the decimal dot). Runge–Kutta schemes are the most
common workhorse in this situation. Systems and libraries like
digits after the decimal dot). Runge–Kutta schemes are the most
common workhorse in this situation. Systems and libraries like
The certification problem has already been addressed in previous works [15, 1, 12, 16], but most implementations are restricted to double or quadruple precision and numerically stable systems without singularities. Developing more general reliable numerical integrators remains a major challenge [17, 18], especially for modern safety-critical applications, including reachability problems [2, 5, 4].
Methodology
We will restrict to the frequent case where  is
a polynomial or a rational function. Then Cauchy–Kovalevskaya's
theorem implies that (1) admits a unique analytic
solution in a neighborhood of
is
a polynomial or a rational function. Then Cauchy–Kovalevskaya's
theorem implies that (1) admits a unique analytic
solution in a neighborhood of  , provided that
our initial condition is non-singular.
, provided that
our initial condition is non-singular.
The initial task of the PhD will consist in studying the existing literature [15, 1, 12, 16], including work on this topic within the MAX team [10, 9, 14, 11, 13, 8].
Then, the thesis will be organized around two lines of progress:
-
Determine the complexity of the reliable integration of
(1) . -
Develop and implement an efficient reliable integrator.
The first line is mostly of theoretical nature: understanding the
computational complexity to reliably solve  ,
the integration path
,
the integration path 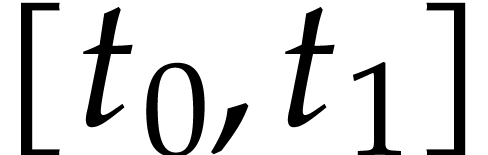 , and specific properties
of the system. State of the art theory can deal with the special case
of non-stiff ODEs (the Jacobian
, and specific properties
of the system. State of the art theory can deal with the special case
of non-stiff ODEs (the Jacobian 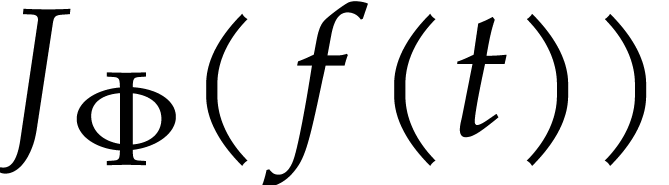 does not
become “too large”) and short paths
does not
become “too large”) and short paths 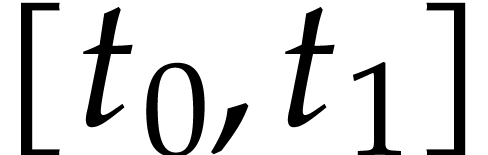 that are far from the singularities of
that are far from the singularities of 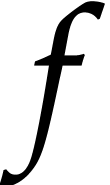 . But a
general theory is still missing.
. But a
general theory is still missing.
The second line is more practical: the new reliable algorithm will be put into practice for machine and then higher precisions. On the one hand this will include the development an ad hoc robust ball arithmetic to certify computations, in the vein of [11]. On the other hand the use of instruction level parallelism (e.g. AVX instructions for x86_64 platforms) and just-in-time compilation will be necessary to attain good computational timings. If time allows, multi-threading issues will be addressed, especially for the certification steps. Let us mention that the parallelizaton of integrators is not fully possible due to their intrinsic sequential nature.
Software implementations will be open source and done in C++ and/or
Expected results
The theoretical part of the research should lead to two or three articles devoted to the new complexity bounds for reliable integration, parametrized in terms of condition numbers related to the system and the solutions.
The practical part of the PhD is expected to lead to a high-level solver that automatically selects the most efficient low-level method(s) for solving the specific input problem. In particular, it should not require any manual fine-tuning of parameters or verifications that we are indeed in a zone where numerical correctness is guaranteed. As said, such an integrator library will constitute a major advance with respect to the existing software. This software implementation may be published in dedicated journals and conferences in the areas of computer algebra and reliable computing.
In order be adopted for safety-critical R&D applications, the new reliable integrator library should not be much slower than the standard purely numerical software. This goal will be achieved by using known and new techniques from High Performance Computing. The final software library is expected to be presented in a wide audience journal such as ACM Transactions on Mathematical Software.
Bibliography
- [1]
-
M. Berz. Cosy infinity version 8 reference manual. Technical Report MSUCL-1088, Michigan State University, East Lansing, 1998.
- [2]
-
Sergiy Bogomolov, Marcelo Forets, Goran Frehse, Kostiantyn Potomkin, and Christian Schilling. Juliareach: a toolbox for set-based reachability. In Proceedings of the 22nd ACM International Conference on Hybrid Systems: Computation and Control, HSCC '19, pages 39–44. New York, NY, USA, 2019. ACM.
- [3]
-
J. C. Butcher. Numerical methods for ordinary differential equations. Wiley, Chichester, second edition, 2008.
- [4]
-
Xin Chen and Sriram Sankaranarayanan. Decomposed reachability analysis for nonlinear systems. In 2016 IEEE Real-Time Systems Symposium (RTSS), pages 13–24. 2016.
- [5]
-
Chuchu Fan, Bolun Qi, Sayan Mitra, Mahesh Viswanathan, and Parasara Sridhar Duggirala. Automatic reachability analysis for nonlinear hybrid models with C2E2. In Swarat Chaudhuri and Azadeh Farzan, editors, Computer Aided Verification, pages 531–538. Cham, 2016. Springer International Publishing.
- [6]
-
E. Hairer, S. P. Nørsett, and G. Wanner. Solving ordinary differential equations I. Nonstiff problems. Springer, Second edition, 1993.
- [7]
-
A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker, and C. S. Woodward. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Transactions on Mathematical Software, 31(3):363–396, sep 2005.
- [8]
-
J. van der Hoeven. Certifying trajectories of dynamical systems. In I. Kotsireas, S. Rump, and C. Yap, editors, Mathematical Aspects of Computer and Information Sciences: 6th International Conference, MACIS 2015, Berlin, Germany, November 11-13, 2015, Revised Selected Papers, pages 520–532. Cham, 2016. Springer International Publishing.
- [9]
-
J. van der Hoeven. Multiple precision floating-point arithmetic on SIMD processors. In 24th IEEE Symposium on Computer Arithmetic (ARITH), pages 2–9. July 2017.
- [10]
-
J. van der Hoeven and G. Lecerf. Faster FFTs in medium precision. In 22nd IEEE Symposium on Computer Arithmetic (ARITH), pages 75–82. June 2015.
- [11]
-
J. van der Hoeven and G. Lecerf. Evaluating straight-line programs over balls. In P. Montuschi, M. Schulte, J. Hormigo, S. Oberman, and N. Revol, editors, 2016 IEEE 23nd Symposium on Computer Arithmetic, pages 142–149. IEEE, 2016.
- [12]
-
T. Kapela, M. Mrozek, D. Wilczak, and P. Zgliczyński. CAPD::DynSys: A flexible C++ toolbox for rigorous numerical analysis of dynamical systems. Communications in Nonlinear Science and Numerical Simulation, 101:105578, oct 2021.
- [13]
-
G. Lecerf. Mathemagix: towards large scale programming for symbolic and certified numeric computations. In K. Fukuda, J. van der Hoeven, M. Joswig, and N. Takayama, editors, Mathematical Software - ICMS 2010, Third International Congress on Mathematical Software, Kobe, Japan, September 13-17, 2010, volume 6327 of Lecture Notes in Computer Science, pages 329–332. Springer, 2010.
- [14]
-
G. Lecerf and J. Saadé. A short survey on Kantorovich-like theorems for Newton's method. ACM Commun. Comput. Algebra, 50(1):1–11, 2016.
- [15]
-
R. E. Moore. Automatic local coordinate transformations to reduce the growth of error bounds in interval computation of solutions to ordinary differential equation. In L. B. Rall, editor, Error in Digital Computation, volume 2, pages 103–140. John Wiley, 1965.
- [16]
-
N. S. Nedialkov. VNODE-LP. Technical Report TR CAS-06-06-NN, Dept. of Computing and Software, McMaster Univ., 2006.
- [17]
-
A. Neumaier. “grand challenge” interval problems. https://www.cs.upc.edu/~robert/mirror/interval-comp/neum02.html, 2002.
- [18]
-
A. Neumaier. Grand challenges and scientific standards in interval analysis. Reliable Computing, 8:313–320, 2002.
- [19]
-
W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical Recipes, The Art of Scientific Computing. Cambridge University Press, 3rd edition, 2007.
- [20]
-
C. Rackauckas and Q. Nie. DifferentialEquations.jl – a performant and feature-rich ecosystem for solving differential equations in Julia. Journal of Open Research Software, 5(1), 2017.
- [21]
-
L. F. Shampine and M. W. Reichelt. The MATLAB ODE Suite. SIAM Journal on Scientific Computing, 18(1):1–22, jan 1997.
This webpage is part of the