PhD proposal 2024–2027

Title: Homotopy methods for differential algebra

Keywords: symbolic and numeric algorithms; differential algebra; sparse interpolation

Contacts

Applying

Applications should comprise a CV, a transcript of records, a letter of motivation, and optional recommendation letters. They should be sent to Joris van der Hoeven before April 15, 2024.

Address

Director of the laboratory: Mr Gilles Schaeffer (schaeffe@lix.polytechnique.fr)

Research team: MAX, Algebraic modeling and symbolic computation

M2 students majoring in computer science or mathematics may apply. Knowledge in at least one of the following topics is required: complexity theory, differential calculus, commutative algebra, computer algebra.

Description

How to predict planetary motion, the spread of an epidemic, or the evolution of a chemical reaction network? Here are some of the many problems that can be modeled by ordinary differential equations (ODEs). The resolution of such equations has a long history and remains an important problem in science and technology.

Differential algebra is a branch of both mathematics and computer science that is concerned with the study of differential equations from a symbolic and computational point of view. The idea is to use the algebraic methods like rewriting or variable elimination to simplify or transform differential equations. Consider, for example, the statement “there is a linear dependence between functions 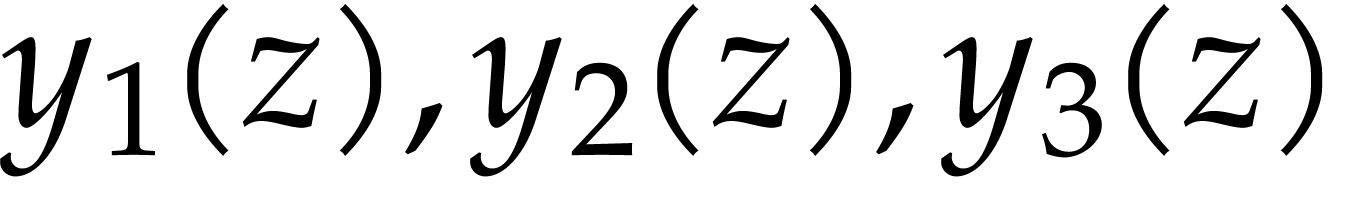with constant coefficients”. This statement can be written as

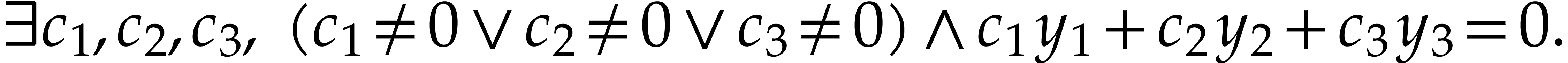
Fundamental theorems in differential algebra guarantee that the existential quantifier can be eliminated: the condition can be expressed as a logical combination of equations and inequations involving only 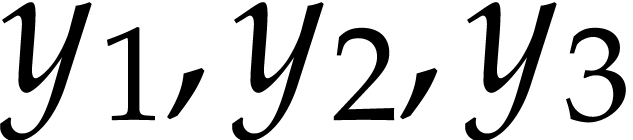. In this case, the condition is indeed equivalent to the vanishing of the Wronskian of :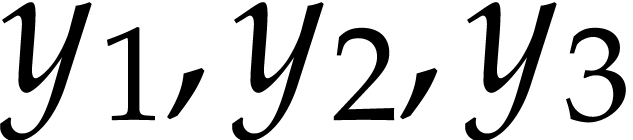

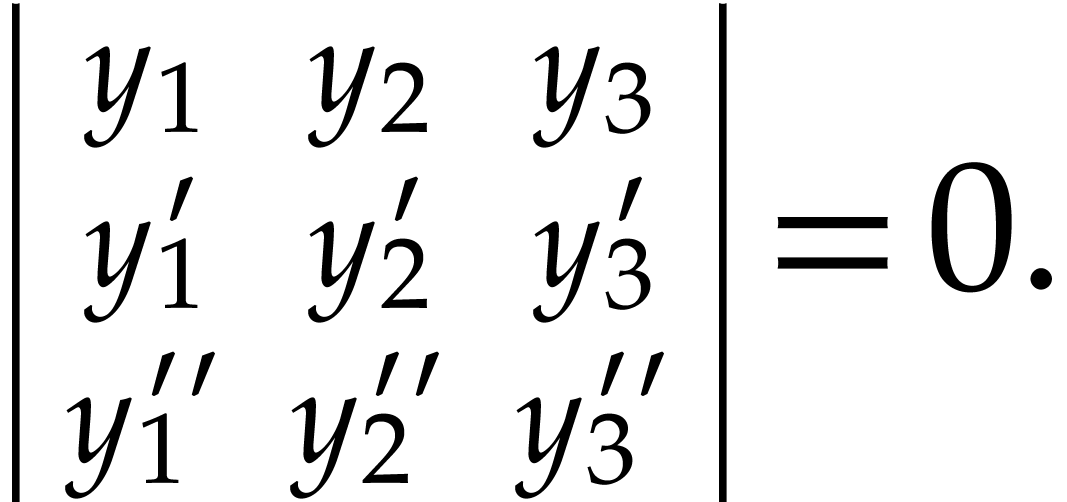
Furthermore, algorithms have been developed and implemented for this kind of quantifier elimination and other fundamental tasks from differential algebra [3, 4, 15].

The traditional approach to differential algebra is to reason on the differential equations themselves as symbolic expressions. One of the drawback of this approach is that the intermediate results of computation may be really large expressions (imagine differentiating the product 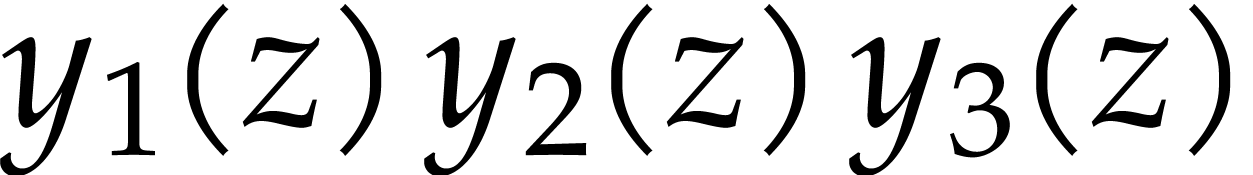ten times!). The aim of the present proposal is to systematically work with power series solutions instead. Such solutions are uniquely determined by the differential equations and a sufficient number of initial conditions. For instance, the power series solutions of are 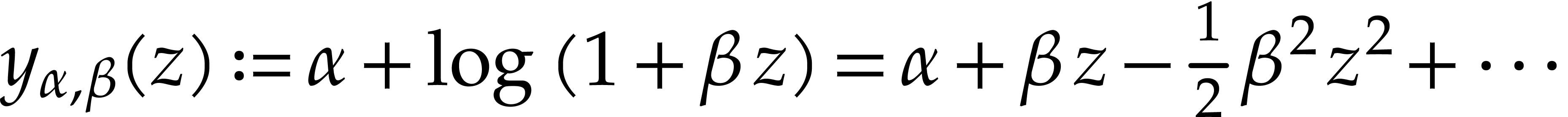, with initial conditions 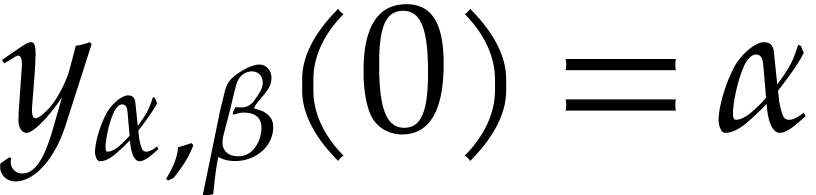, 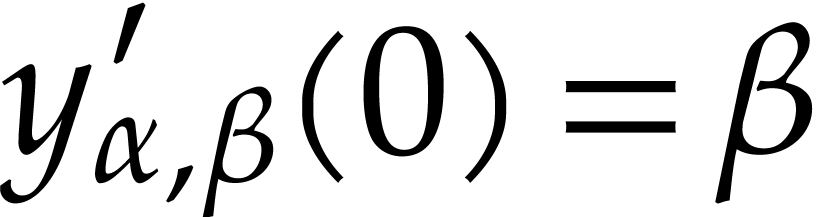. Inversely, any differential equation of which 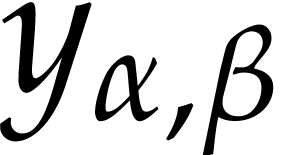is a solution is a logical consequence of .

Using this point of view, systems of differential equations give rise to systems of algebraic equations on power series coefficients. For instance, the equation in 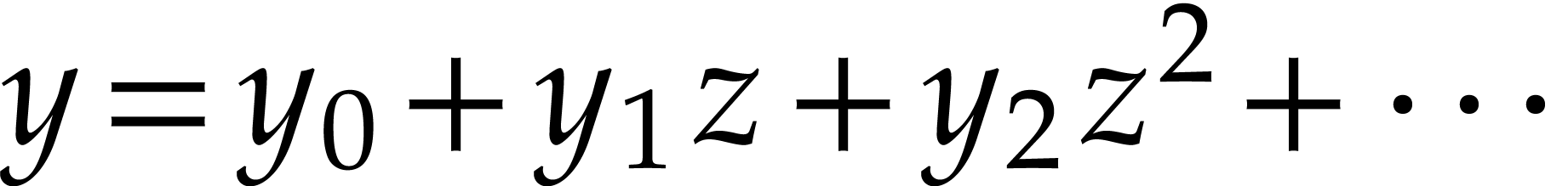is equivalent to the infinite system of equations 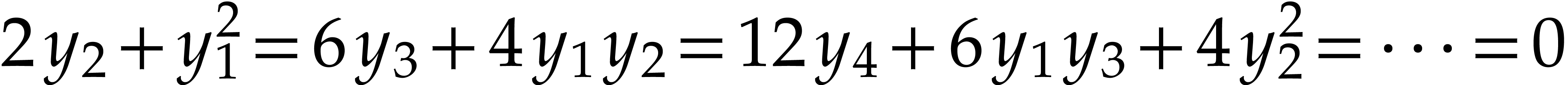in 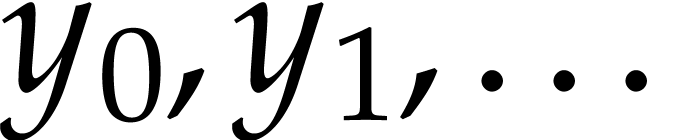. Truncations of such systems can be solved using numerical homotopies. This means that we study the effect of small perturbations of the initial conditions 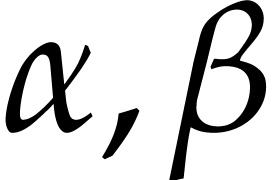on the solution 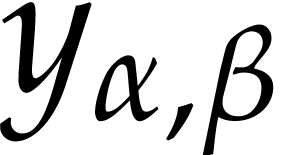. We may also consider deformations of the equations themselves into equations that are typically easier to solve.

When successful, numeric homotopy techniques allow us to determine numeric power series solutions for our original system of differential equations. A final challenge is to recover the simplest differential equation(s) of which these numeric power series are the solution. This typically yields a simplification of the original system of differential equations or new equations that do not involve some of the unknown functions. We plan to combine homotopy continuation and sparse interpolation techniques in order to compute differential equations satisfied by power series solutions.

In summary, the main objective of the thesis is to build a bridge between differential algebra and numerical descriptions of sets of power series solutions to differential equations. This bridge should be as effective as possible and lead to new, more efficient algorithms for typical problems from differential algebra, such as the simplification of systems of differential equations, quantifier elimination, uncovering hidden constraints, or the identification of parameters. Depending on her or his profile, the candidate may put higher focus on the more theoretical or practical aspects of this program.

Context

Differential algebra was initially created by Ritt [14], Kolchin [11], and others [18, 17] as a purely algebraic and constructive theory to reason on systems of differential equations. With the advent of computer algebra, effective counterparts have been developed and implemented [3, 4, 15]. The approach to study differential equations through their power series solutions goes back to Ehresmann [5, 12, 13], but effective counterparts are scarce [21].

Numerical homotopy techniques have led to very efficient solvers for systems of algebraic equations [20, 1, 6]. However, they are typically less robust than algebraic solvers and the development of solvers that are both reliable and efficient remains an important issue [2, 7, 19].

Sparse interpolation [16] is an approach to recover sparse polynomials or rational functions from sufficiently many numerical evaluations. Due to a series of recent improvements [8, 10, 9], it has become very efficient. Its combination with numerical homotopy techniques, it may both lead to more robust solvers and the reconstruction of algebraic counterparts of numerical solutions.

Methodology

We seek for excellent candidates with a strong scholarship both in mathematics and computer science. The required theoretical knowledge mostly concerns computer algebra, commutative algebra, and rudiments in complex analysis. General skills in computer science are needed to contribute to efficient implementations.

The thesis will begin with a review of current algorithms for solving algebraic systems through homotopy continuation and sparse interpolation. The PhD student will then apply this to the resolution of algebraic systems of equations that arise as constraints on the coefficients of power series solutions to systems of differential equations.

Software implementations will be open source and part of or compatible with the Mathemagix system (see http://www.mathemagix.org). Depending on her or his profile, the PhD student may chose to put greater emphasize on the theoretical or practical aspects of the project.

Expected results

The theoretical part of the research should lead to two or three articles, describing an effective bridge between differential algebra and numerical power series solutions of systems of differential equations, while analyzing the complexity of this approach.

The practical part of the PhD is expected to lead to a new algebraic solver of systems of differential equations. This may include the development of a polynomial system solver, based on reliable numerical homotopies, and software for sparse interpolation.

The software should be open source and usable from within the Mathemagix system. We expect it to be presented at the ISSAC conference and/or a journal like ACM Transactions on Mathematical Software or SIAM Journal on Applied Dynamical Systems.

Bibliography

[1]

D. J. Bates, J. D. Hauenstein, A. J. Sommese, and C. W. Wampler. Numerically Solving Polynomial Systems with Bertini. SIAM, 2013.

[2]

C. Beltrán and A. Leykin. Certified numerical homotopy tracking. Experiment. Math., 21(1):69–83, 2012.

[3]

F. Boulier, D. Lazard, F. Ollivier, and M. Petitot. Representation for the radical of a finitely generated differential ideal. In Proc. ISSAC '95, pages 158–166. New York, NY, USA, 1995. ACM.

[4]

F. Boulier, D. Lazard, F. Ollivier, and M. Petitot. Computing representations for radicals of finitely generated differential ideals. AAECC, 20:73–121, 2009.

[5]

Ch. Ehresmann. Introduction à la théorie des structures infinitésimales et des pseudo-groupes de Lie. In Géometrie Différentielle, Colloq. Inter. du Centre Nat. de la Rech. Sci., Strasbourg, pages 97–110. 1953.

[6]

J. D. Hauenstein and A. J. Sommese. What is numerical algebraic geometry? Journal of Symbolic Computation, 79(3):499–507, 2017.

[7]

J. van der Hoeven. Reliable homotopy continuation. Technical Report, HAL, 2011. https://hal.archives-ouvertes.fr/hal-00589948.

[8]

J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation in practice. ACM Commun. Comput. Algebra, 48(3/4):187–191, 2015.

[9]

J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation. Exploring fast heuristic algorithms over finite fields. Technical Report, HAL, 2019. https://hal.archives-ouvertes.fr/hal-02382117.

[10]

J. van der Hoeven and M. Monagan. Computing one billion roots using the tangent Graeffe method. ACM SIGSAM Commun. Comput. Algebra, 54(3):65–85, 2021.

[11]

E. R. Kolchin. Differential algebra and algebraic groups. Academic Press, New York, 1973.

[12]

V.V. Krasil'shchik, V.V. Lychagin, and A.M. Vinogradov. Geometry of Jet Spaces and Nonlinear Partial Differential Equations. Gordon and Breach, New York, 1986.

[13]

P. J. Olver. Equivalence, Invariants and Symmetry. Cambridge University Press, 1995.

[14]

J. F. Ritt. Differential algebra. Amer. Math. Soc., New York, 1950.

[15]

D. Robertz. Formal Algorithmic Elimination for PDEs, volume 2121 of Lecture Notres in Mathematics. Springer, Cham, 2014.

[16]

D. S. Roche. What can (and can't) we do with sparse polynomials? In Proc. ISSAC '18, pages 25–30. New York, NY, USA, 2018. ACM.

[17]

A. Rosenfeld. Specializations in differential algebra. Trans. Amer. Math. Soc., 90:394–407, 1959.

[18]

A. Seidenberg. An elimination theorem for differential algebra. Univ. California Publ. Math. (N.S.), pages 31–38, 1956.

[19]

S. Telen, M. Van Barel, and J. Verschelde. A robust numerical path tracking algorithm for polynomial homotopy continuation. SIAM Journal on Scientific Computing, 42(6):0, 2020.

[20]

J. Verschelde. PHCpack: a general-purpose solver for polynomial systems by homotopy continuation. ACM Transactions on Mathematical Software, 25(2):251–276, 1999. Algorithm 795.

[21]

W. Wu, G. Reid, and O. Golubitsky. Towards Geometric Completion of Differential Systems by Points, pages 79–97. Springer Vienna, 2010.