 |
Reliable numerical integration |  |
M2 internship proposal 2023–2024
Title: Reliable numerical integration
Topics: symbolic and numeric algorithms, reliable computing, integrators
Address
Director of the laboratory: Mr Gilles Schaeffer (schaeffe@lix.polytechnique.fr)
Research team: MAX, Algebraic modeling and symbolic computation
Contacts
Context
The MAX team is searching for PhD candidates on the themes of the ANR “NODE” project. The present M2 internship proposal allows applicants to familiarize themselves with these themes. Upon successful completion of the internship, there will be an opportunity to pursue with a PhD. The ANR NODE project provides funding for two PhD grants.
Description
How to predict planetary motion, the spread of an epidemic, or the evolution of a chemical reaction network? Here are some of the many problems that can be modeled by ordinary differential equations (ODEs). The resolution of such equations has a long history and remains an important problem in science and technology.
 |
(1) |
where 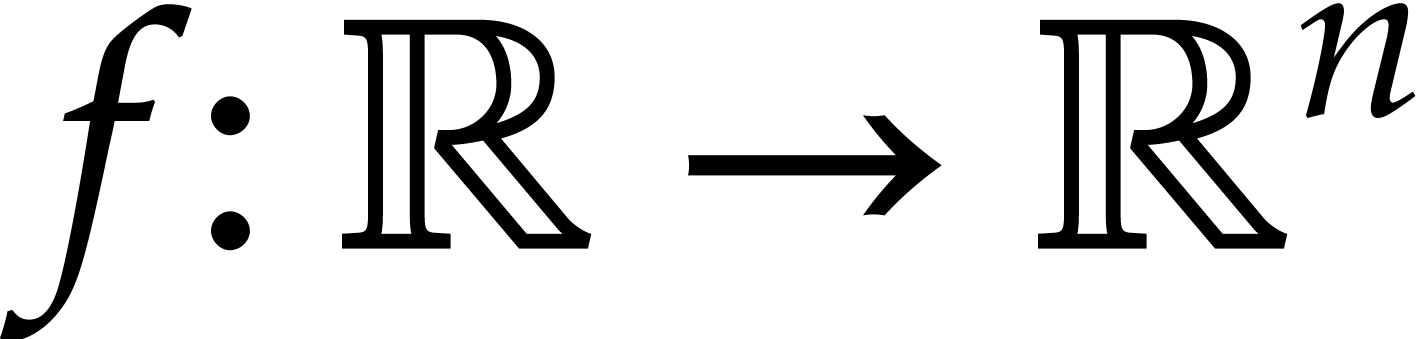 ,
, 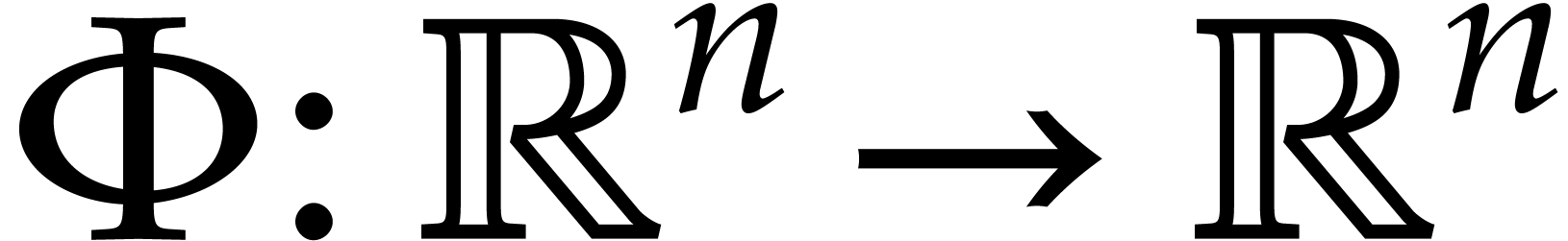 , and an initial
condition is provided at
, and an initial
condition is provided at  . The numeric
integration of such a system is a widely studied problem in numeric
analysis. The function
. The numeric
integration of such a system is a widely studied problem in numeric
analysis. The function  can usually be an
arbitrary smooth function and the integration is typically done with
machine precision. Runge–Kutta schemes are the most common
workhorse in this situation [2, 3, 12].
Systems and libraries like
can usually be an
arbitrary smooth function and the integration is typically done with
machine precision. Runge–Kutta schemes are the most common
workhorse in this situation [2, 3, 12].
Systems and libraries like
This internship concerns the certification problem: given  and
and  such that (1)
can be integrated on
such that (1)
can be integrated on 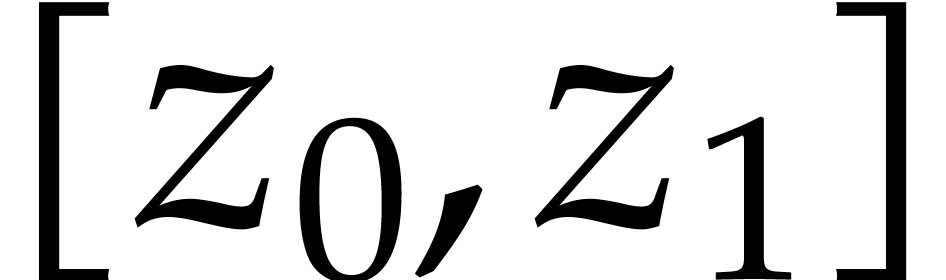 , how to compute an
approximation
, how to compute an
approximation 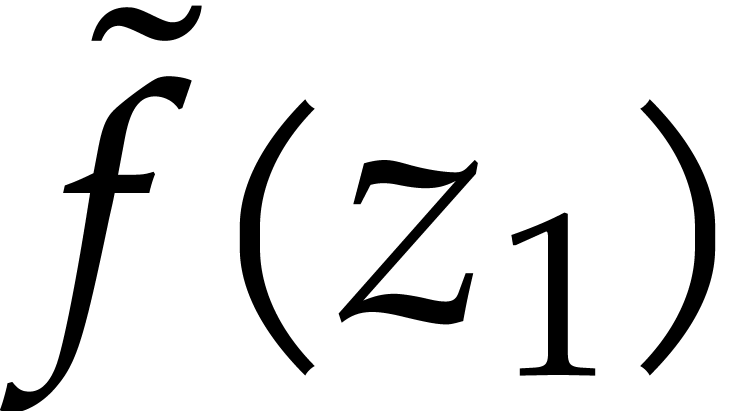 of
of 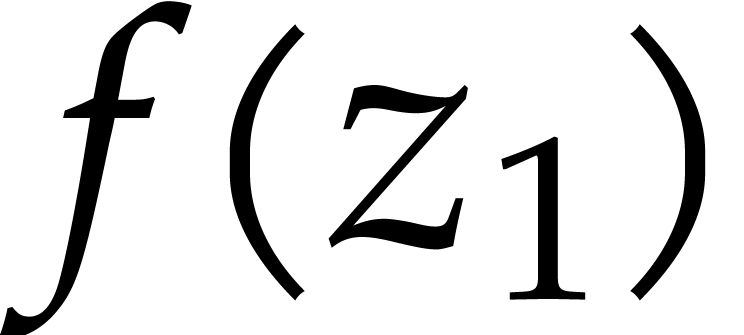 with
with
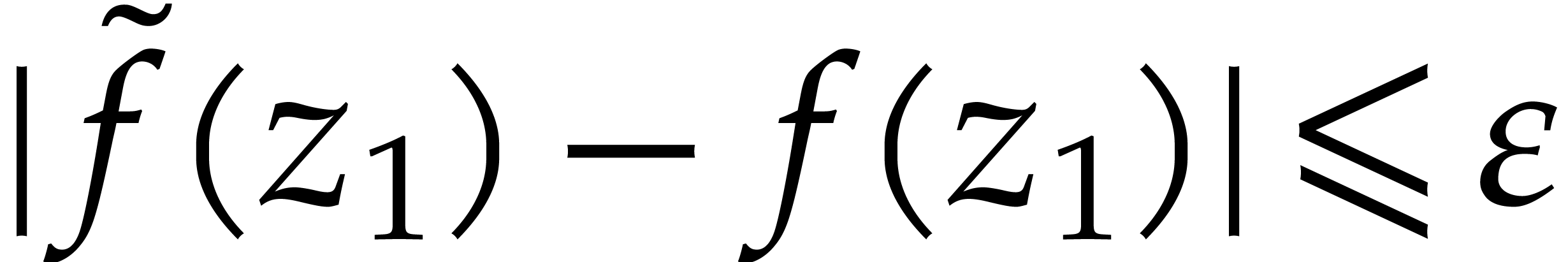 . There exist several software packages for
this task [1, 9, 11], most
which implement certified numerical schemes that are based on Taylor
series expansions. For efficiency reasons, one might prefer certified
counterparts of more traditional Runge–Kutta integrators.
. There exist several software packages for
this task [1, 9, 11], most
which implement certified numerical schemes that are based on Taylor
series expansions. For efficiency reasons, one might prefer certified
counterparts of more traditional Runge–Kutta integrators.
The aim of the present internship proposal is the development and
implementation of reliable counterparts of traditional
Runge–Kutta schemes. Implementations will be done in C++ within
the
One popular approach to reliable computation is to use interval or
ball arithmetic [10, 5, 8, 7]. This amounts to systematically replace any floating
point approximation 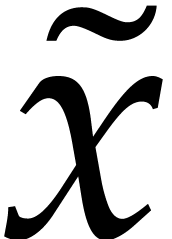 of a real number
of a real number  by an interval
by an interval 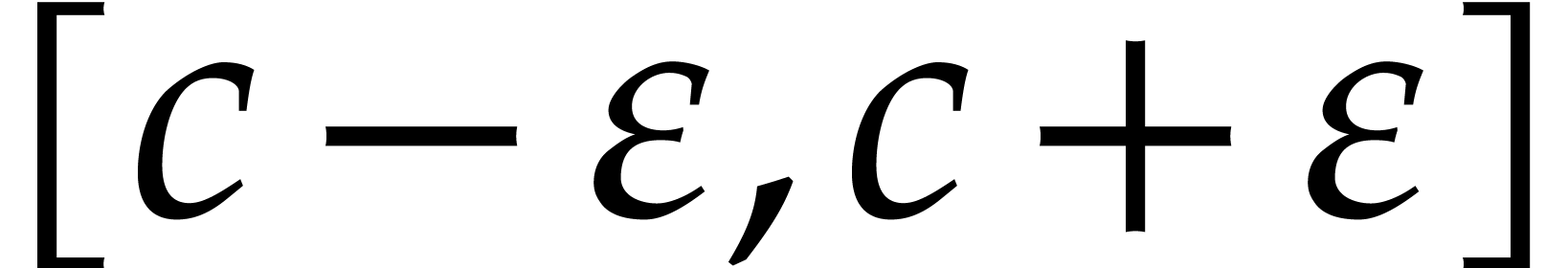 that is certified
to contain the exact value
that is certified
to contain the exact value  . There is a
trade-off between the efficiency of operations for this kind of
arithmetic and the quality
. There is a
trade-off between the efficiency of operations for this kind of
arithmetic and the quality  of the error bounds
[6]. We aim to develop interval and ball versions of
Runge–Kutta schemes that are both efficient and accurate
(i.e. the produced error bounds
of the error bounds
[6]. We aim to develop interval and ball versions of
Runge–Kutta schemes that are both efficient and accurate
(i.e. the produced error bounds  are as small as possible).
are as small as possible).
We seek for excellent candidates with a background both in mathematics and computer science. Applicants will be required to have knowledge in complex analysis, differential equations, algorithms. Skills in computer science will be needed to achieve efficient implementations in C++.
Bibliography
- [1]
-
M. Berz. Cosy infinity version 8 reference manual. Technical Report MSUCL-1088, Michigan State University, East Lansing, 1998.
- [2]
-
J. C. Butcher. Numerical methods for ordinary differential equations. Wiley, Chichester, second edition, 2008.
- [3]
-
E. Hairer, S. P. Nørsett, and G. Wanner. Solving ordinary differential equations I. Nonstiff problems. Springer, Second edition, 1993.
- [4]
-
A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker, and C. S. Woodward. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Transactions on Mathematical Software, 31(3):363–396, sep 2005.
- [5]
-
J. van der Hoeven. Ball arithmetic. Technical Report, HAL, 2009. https://hal.archives-ouvertes.fr/hal-00432152.
- [6]
-
J. van der Hoeven. Journées Nationales de Calcul Formel (2011), volume 2 of Les cours du CIRM, chapter Calcul analytique. CEDRAM, 2011. Exp. No. 4, 85 pages, http://ccirm.cedram.org/ccirm-bin/fitem?id=CCIRM_2011__2_1_A4_0.
- [7]
-
J. van der Hoeven and G. Lecerf. Evaluating straight-line programs over balls. In Paolo Montuschi, Michael Schulte, Javier Hormigo, Stuart Oberman, and Nathalie Revol, editors, 2016 IEEE 23nd Symposium on Computer Arithmetic, pages 142–149. IEEE, 2016.
- [8]
-
F. Johansson. Arb: a C library for ball arithmetic. ACM Commun. Comput. Algebra, 47(3/4):166–169, 2014.
- [9]
-
T. Kapela, M. Mrozek, D. Wilczak, and P. Zgliczyński. CAPD::DynSys: A flexible C++ toolbox for rigorous numerical analysis of dynamical systems. Communications in Nonlinear Science and Numerical Simulation, 101:105578, oct 2021.
- [10]
-
R. E. Moore. Automatic local coordinate transformations to reduce the growth of error bounds in interval computation of solutions to ordinary differential equation. In L. B. Rall, editor, Error in Digital Computation, volume 2, pages 103–140. John Wiley, 1965.
- [11]
-
N. S. Nedialkov. VNODE-LP. Technical Report TR CAS-06-06-NN, Dept. of Computing and Software, McMaster Univ., 2006.
- [12]
-
W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical Recipes, The Art of Scientific Computing. Cambridge University Press, 3rd edition, 2007.
- [13]
-
C. Rackauckas and Q. Nie. DifferentialEquations.jl – a performant and feature-rich ecosystem for solving differential equations in Julia. Journal of Open Research Software, 5(1), 2017.
- [14]
-
L. F. Shampine and M. W. Reichelt. The MATLAB ODE Suite. SIAM Journal on Scientific Computing, 18(1):1–22, jan 1997.
This webpage is part of the