M2 internship proposal 2023–2024

Title: Numerical approach of generalized flatness

Topics: symbolic-numeric computation, modeling

Address

Director of the laboratory: Mr Gilles Schaeffer (schaeffe@lix.polytechnique.fr)

Research team: MAX, Algebraic modeling and symbolic computation

Contacts

Context

The MAX team is searching for PhD candidates on the themes of the ANR “NODE” project. The present M2 internship proposal allows applicants to familiarize themselves with these themes. Upon successful completion of the internship, there will be an opportunity to pursue with a PhD. The ANR NODE project provides funding for two PhD grants.

Description

Consider a dynamical system that is modeled by a system of ordinary differential equations (ODEs)

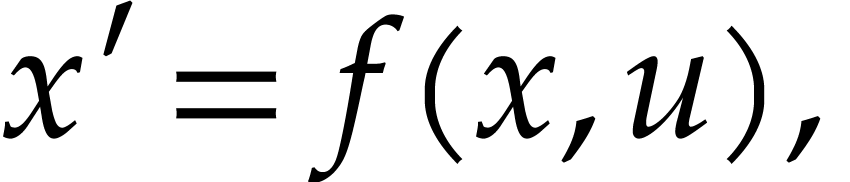(1)

where 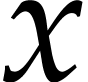is a vector of state functions (describing the current state of the system) and 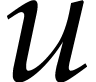is a vector of control functions (that are controlled by the user).

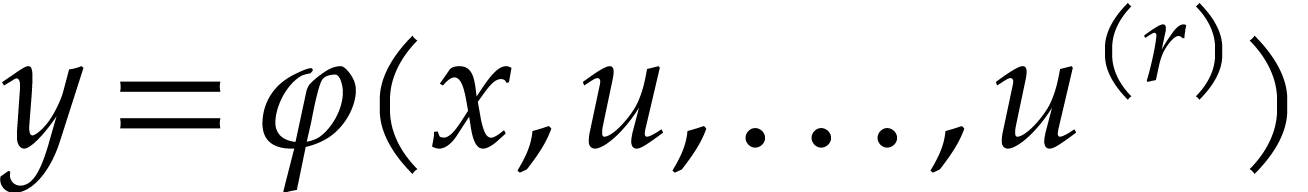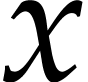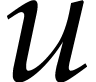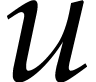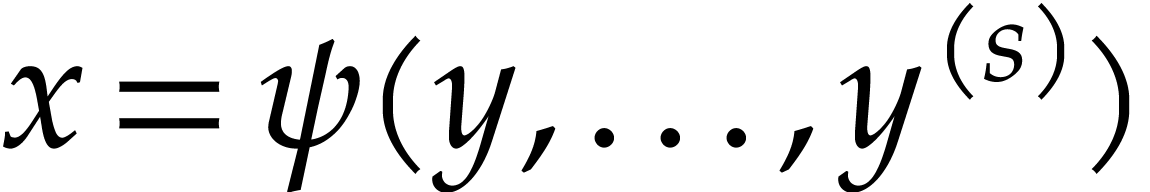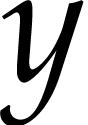The system (1) is said to be flat [1] if there exists a so-called flat output that can be expressed in terms of , , and a finite number of derivatives of , and such that both and can be expressed in terms of and a finite number of its derivatives. Moreover, we require that 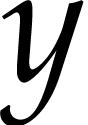satisfies no non-trivial differential equation of the form .

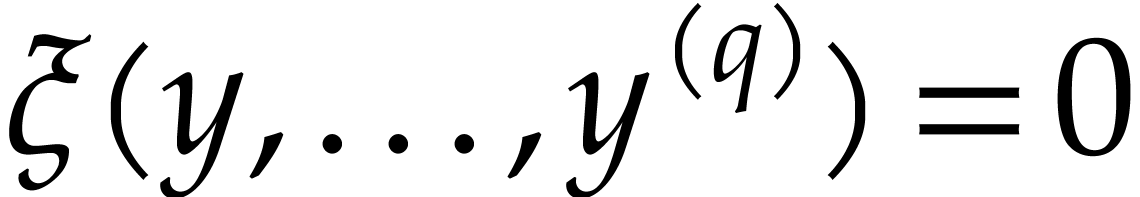The flatness property greatly facilitates motion planning, that is to design a control to go from a given starting point to a given goal. A car is a classical example of flat system, for which the coordinates of any point of the rear axis is a flat output.

Generic systems are not flat, but flatness is ubiquitous in engineering [3]. This may require some simplifications of the model. For examples, a classical aircraft model is flat if one neglects the thrusts created by the actuators (ailerons, elevators, rudder) [4]. Flatness makes also easier to design a feed-back that can compensate perturbations but also to model errors [2].

In a recent paper, it has been proposed to improve the flat control of an aircraft by using the values of the thrusts due to the actuators, provided by the classical flat parametrization, to design a new more accurate parametrization [5]. This process can be iterated to produce a very precise motion planning for the aircraft model without simplification.

The order of derivatives of the flat outputs required for such a parametrization increases with the number of iterations, so that this generalized flat parametrization depends potentially of an infinite number of derivatives. One may conjecture that all systems would be flat allowing functions of an infinite number of derivatives.

The goal of the internship is to investigate this notion of generalized flatness, using computer experiments. On may consider first a car with two trailers that is flat if the trailers are attached just above the rear axis, but not in the general case [6]. A generalized flat parametrization may be designed using iterations or homotopy methods, that is slowly moving the points where trailers are attached.

One may take advantage of existing implementations in Maple for the aircraft and/or use the more efficient tools provided by Mathemagix. The second half of the internship can be devoted to more ambitious implementations or to theoretical investigations, such as proofs of convergence.

Bibliography