M2 internship proposal 2023–2024

Title: Numerical approach to structural parameter identifiability

Topics: symbolic-numeric computation, modeling

Address

Director of the laboratory: Mr Gilles Schaeffer (schaeffe@lix.polytechnique.fr)

Research team: MAX, Algebraic modeling and symbolic computation

Contacts

Context

The MAX team is searching for PhD candidates on the themes of the ANR “NODE” project. The present M2 internship proposal allows applicants to familiarize themselves with these themes. Upon successful completion of the internship, there will be an opportunity to pursue with a PhD. The ANR NODE project provides funding for two PhD grants.

Description

Consider a dynamical system model described by a parametric system of ordinary differential equations (ODEs)

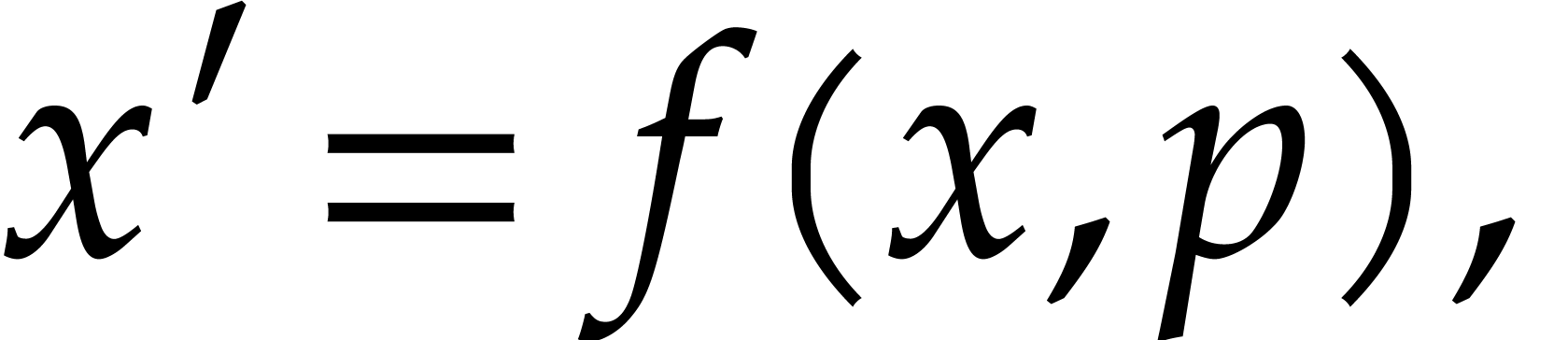
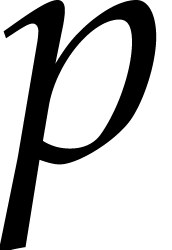where is a vector of unknown functions and is a vector of scalar parameters. Once such a model has been derived, typically, the next step is to calibrate it by inferring the parameter values from experimental data. In most cases, experimental data is available only for a subset of 's, so the information contained in the data may be insufficient for an unambiguous inference of the values of 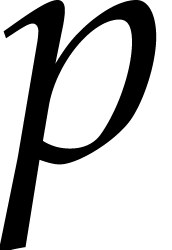's. If this is the case, the model is said to be structurally non-identifiable. Since structural identifiability is a property of the model and the set of states for which data is available, it is desirable to check this property before conducting costly experiments.

Several tools for assessing structural identifiability are available (see a recent survey[1]). The bottleneck for all of them is manipulation with large polynomial systems arising from the original ODE model. For example, SIAN [2], one of the state of the art tools, reduces the identifiability assessment to counting roots of a large polynomial system. This root counting is performed using purely symbolic methods that do not scale well.

The aim of the internship is to replace symbolic algorithms for polynomial system solving in SIAN with numeric algorithms based on homotopy continuation [3] (for a short introduction with examples, see this webpage). Homotopy continuation methods yield a large family of algorithms, so finding the appropriate algorithm and fine-tuning it to a polynomial system at hand is always a nontrivial task. Thus, the main challenge of the internship will be how to exploit the “differential nature” of the polynomial system to make this numeric computation efficient and robust.

Bibliography